上海市闸北区高三下学期期中练习(二模)文科数学试卷
设复数 ,在复平面的对应的向量分别为
,在复平面的对应的向量分别为 ,则向量
,则向量 对应的复数所对应的点的坐标为____________.
对应的复数所对应的点的坐标为____________.
若二项式 展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________.
展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________.
从双曲线 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于点
交双曲线右支于点 ,若
,若 是线段
是线段 的中点,
的中点, 为原点,则
为原点,则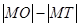 的值是____________.
的值是____________.
已知集合 ,
,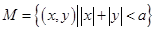 ,
, ,现给出下列函数:①
,现给出下列函数:① ;②
;② ;③
;③ ;④
;④ .若
.若 时,恒有
时,恒有 ,则所有满足条件的函数
,则所有满足条件的函数 的编号是____________.
的编号是____________.
下列命题中,正确的个数是
(1)直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
(2)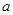 、
、 为异面直线,则过
为异面直线,则过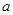 且与
且与 平行的平面有且仅有一个;
平行的平面有且仅有一个;
(3)直四棱柱是直平行六面体;
(4)两相邻侧面所成角相等的棱锥是正棱锥.
| A.0 | B.1 | C.2 | D.3 |
如图,下列四个几何题中,它们的三视图(主视图、俯视图、侧视图)有且仅有两个相同,而另一个不同的两个几何体是

(1)棱长为2的正方体 (2)底面直径和高均为2的圆柱
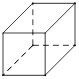
(3)底面直径和高均为2的圆锥 (4)底面边长为2高为2的直平行六面体
| A.(1)、(2) | B.(1)、(3) | C.(2)、(3) | D.(1)、(4) |
(本题满分12分,第(1)小题5分,第(2)小题7分)
如图, 是圆柱体
是圆柱体 的一条母线,已知
的一条母线,已知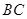 过底面圆的圆心
过底面圆的圆心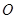 ,
, 是圆
是圆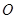 上不与点
上不与点 重合的任意一点,
重合的任意一点, ,
, ,
, .
.
(1)求直线 与直线
与直线 所成角的大小;
所成角的大小;
(2)将四面体 绕母线
绕母线 旋转一周,求
旋转一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
(本题满分14分,第(1)、(2)小题各3分;第(3)、(4)小题各4分)
请你指出函数
 的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
(1)当 时,等式
时,等式 恒成立;
恒成立;
(2)若 ,则一定有
,则一定有 ;
;
(3)若 ,方程
,方程 有两个不相等的实数解;
有两个不相等的实数解;
(4)函数 在
在 上有三个零点.
上有三个零点.
(本题满分15分,第(1)小题6分,第(2)小题9分)
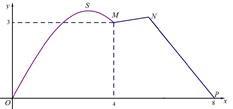
如图所示,某市拟在长为 道路
道路 的一侧修建一条运动赛道,赛道的前一部分为曲线段
的一侧修建一条运动赛道,赛道的前一部分为曲线段 ,该曲线段为函数
,该曲线段为函数
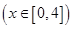 的图像,且图像的最高点为
的图像,且图像的最高点为 ,赛道的后一部分为折线段
,赛道的后一部分为折线段 ,且
,且 .
.
(1)求 、
、 两点间的直线距离;
两点间的直线距离;
(2)求折线段赛道 长度的最大值.
长度的最大值.
(本题满分16分,第(1)小题6分,第(2)小题10分)
已知圆 ,点
,点 ,点
,点 在圆
在圆 上运动,
上运动, 的垂直平分线交
的垂直平分线交 于点
于点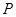 .
.
(1)求动点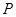 的轨迹
的轨迹 方程;
方程;
(2)过点 且斜率为
且斜率为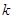 的动直线
的动直线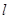 交曲线
交曲线 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,请求出点
为直径的圆恒过这个点?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的图像经过点
的图像经过点 ,则函数
,则函数 满足
满足 如果目标函数
如果目标函数 的最小值为
的最小值为 ,则实数
,则实数 等于____________.
等于____________. 与曲线
与曲线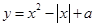 有四个交点,则实数
有四个交点,则实数 的取值范围是____________.
的取值范围是____________.
 的函数
的函数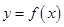 的图像关于点
的图像关于点 对称,
对称,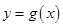 是
是 ,则
,则 ____________.
____________. 数列
数列 的前
的前 项和为
项和为 ,则
,则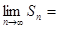 ___________.
___________.
 行的各数之和为
行的各数之和为 ,则
,则
 ,若
,若 ,
, ,则必有
,则必有
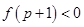

 的符号不能确定
的符号不能确定 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作 ,已知向量列
,已知向量列 ,
, 
 .
.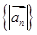 是等比数列;
是等比数列; 表示向量
表示向量 与
与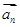 间的夹角,若
间的夹角,若 ,
, ,求
,求 ;
;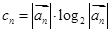 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号