高中数学解答题

设 $\left\{a_n\right\}$ 是等差数列， $a_1=–10$ ，且 $a_2+10$ ， $a_3+8$ ， $a_4+6$ 成等比数列．

（Ⅰ）求 $\left\{a_n\right\}$ 的通项公式；

（Ⅱ）记 $\left\{a_n\right\}$ 的前 n项和为 $S_n$ ，求 $S_n$ 的最小值．

在 $△ABC$ 中， $a=3$ ， $\mathit{b–c}=2$ ， $\mathit{cosB}=-\frac{1}{2}$ ．

（Ⅰ）求 b， c的值；

（Ⅱ）求 $\mathit{sin}（B+C）$ 的值．

在平面直角坐标系 $\mathit{xOy}$ 中，椭圆 $E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，焦距为2．

（Ⅰ）求椭圆E的方程．

（Ⅱ）如图，该直线 $l：y=k_{1}x﹣\frac{\sqrt{3}}{2}$ 交椭圆E于A，B两点，C是椭圆E上的一点，直线OC的斜率为 $k_2$ ， 且看 $k_1{k}_2=\frac{\sqrt{2}}{4}$ ，M是线段OC延长线上一点，且 $\left|\mathit{MC}\right|：\left|\mathit{AB}\right|=2：3$ ，⊙M的半径为 $\left|\mathit{MC}\right|$ ，OS，OT是⊙M的两条切线，切点分别为S，T，求 $\angle \mathit{SOT}$ 的最大值，并求取得最大值时直线l的斜率．

已知函数 $f（x）=x^2+2\mathit{cosx}$ ， $g（x）=e^x（\mathit{cosx}﹣\mathit{sinx}+2x﹣2）$ ，其中 $e\approx 2.17828\dots$ 是自然对数的底数．

（Ⅰ）求曲线 $y=f（x）$ 在点 $\left(\pi ，f\left(\pi \right)\right)$ 处的切线方程；

（Ⅱ）令 $h\left(x\right)=g\left(x\right)\mathit{-}\mathit{a\; f}\left(x\right)\left(a\in R\right)$ ，讨论 $h\left(x\right)$ 的单调性并判断有无极值，有极值时求出极值．

已知 $\left\{x_n\right\}$ 是各项均为正数的等比数列，且 $x_1+x_2=3$ ， $x_3﹣x_2=2$ ．

（Ⅰ）求数列 $\left\{x_n\right\}$ 的通项公式；

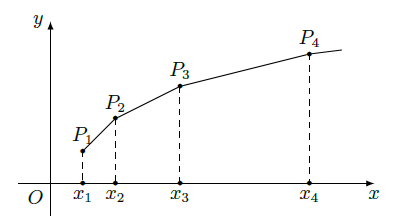
（Ⅱ）如图，在平面直角坐标系 $\mathit{xOy}$ 中，依次连接点 $P_1（x_1\mathit{ }，1）$ ， $P_2（x_2\mathit{ }，2）\dots P_{n+1}（x_{n+1}\mathit{ }，\mathit{n}+1）$ 得到折线 $P1\mathit{P}2\dots P_{n+1}\mathit{ }$ ， 求由该折线与直线 $y=0$ ， $x=x_1\mathit{ }$ ， $\mathit{x}=x_{n+1}$ 所围成的区域的面积 $T_n$ ．

在心理学研究中，常采用对比试验的方法评价不同心理暗示对人的影响，具体方法如下：将参加试验的志愿者随机分成两组，一组接受甲种心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用，现有6名男志愿者A ₁ ， A ₂ ， A ₃ ， A ₄ ， A ₅ ， A ₆和4名女志愿者B ₁ ， B ₂ ， B ₃ ， B ₄ ， 从中随机抽取5人接受甲种心理暗示，另5人接受乙种心理暗示．

（Ⅰ）求接受甲种心理暗示的志愿者中包含A ₁但不包含B ₁的概率．

（Ⅱ）用X表示接受乙种心理暗示的女志愿者人数，求X的分布列与数学期望EX．

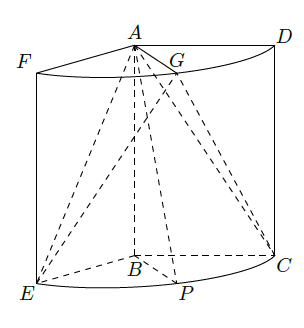
如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是 $\stackrel{̂}{\mathit{DF}}$ 的中点．

（Ⅰ）设P是 $\stackrel{̂}{\mathit{CE}}$ 上的一点，且 $\mathit{AP}\perp \mathit{BE}$ ，求 $\angle \mathit{CBP}$ 的大小；

（Ⅱ）当 $\mathit{AB}=3$ ， $\mathit{AD}=2$ 时，求二面角 $E﹣\mathit{AG}﹣C$ 的大小．

设函数 $f（x）=\mathit{sin}\left(\omega x﹣\frac{\pi }{6}\right)+\mathit{sin}\left(\omega x﹣\frac{\pi }{2}\right)$ ，其中 $0＜\omega ＜3$ ，已知 $f（\frac{\pi }{6}）=0$ ．

（Ⅰ）求 $\omega$ ；

（Ⅱ）将函数 $y=f\left(x\right)$ 的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 $\frac{\pi }{4}$ 个单位，得到函数 $y=g\left(x\right)$ 的图象，求 $g\left(x\right)$ 在 $\left[﹣\frac{\pi }{4}，\frac{3\pi }{4}\right]$ 上的最小值．

[选修4-5：不等式选讲]已知函数 $f\left(x\right)=\mathit{│x}+1\mathit{│–│x–}2│$ .

（1）求不等式 $f\left(x\right)\ge 1$ 的解集；

（2）若不等式 $f\left(x\right)\ge x^2\mathit{–x}+m$ 的解集非空，求实数 m的取值范围.

[选修4―4：坐标系与参数方程]

在直角坐标系 xOy中，直线 $l_1$ 的参数方程为 $\left\{\begin{array}{c}x=2+t,\\ y=\mathit{kt},\end{array}\right.$ （ t为参数），直线 $l_2$ 的参数方程为 $\left\{\begin{array}{c}x=-2+m,\\ y=\frac{m}{k},\end{array}\right.（m\mathit{为参数）}$ .设 l ₁与 l ₂的交点为 P，当 k变化时， P的轨迹为曲线 C ．

（1）写出 C的普通方程；

（2）以坐标原点为极点， x轴正半轴为极轴建立极坐标系，设 $l3：\rho (\mathit{cos}\theta +\mathit{sin\theta })-\sqrt{2}=0$ ， M为 l ₃与 C的交点，求 M的极径.

已知函数 $f\left(x\right)=\mathit{lnx}+a{x}^2+(2a+1)$ x．

（1）讨论 $f\left(x\right)$ 的单调性；

（2）当 $a﹤0$ 时，证明 $f\left(x\right)\le -\frac{3}{4a}-2$ ．

在直角坐标系 $\mathit{xOy}$ 中，曲线 $y=x^2+\mathit{mx}-2$ 与x轴交于A，B两点，点C的坐标为 $(0,1)$ .当m变化时，解答下列问题：

（1）能否出现 $\mathit{AC}\perp \mathit{BC}$ 的情况？说明理由；

（2）证明过 A， B， C三点的圆在 y轴上截得的弦长为定值.

如图，四面体ABCD中，△ABC是正三角形， $\mathit{AD}=\mathit{CD}$ ．

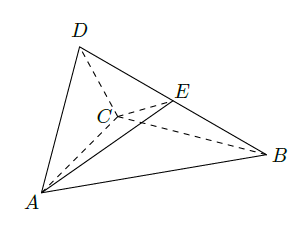
（1）证明： $\mathit{AC}\perp \mathit{BD}$ ；

（2）已知△ACD是直角三角形， $\mathit{AB}=\mathit{BD}$．若E为棱BD上与D不重合的点，且 $\mathit{AE}\perp \mathit{EC}$ ，求四面体ABCE与四面体ACDE的体积比．

某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

最高气温	$[10，15）$	$[15，20）$	$[20，25）$	$[25，30）$	$[30，35）$	$[35，40）$
天数	2	16	36	25	7	4

以最高气温位于各区间的频率代替最高气温位于该区间的概率。

（1）求六月份这种酸奶一天的需求量不超过300瓶的概率；

（2）设六月份一天销售这种酸奶的利润为 $Y$ （单位：元），当六月份这种酸奶一天的进货量为450瓶时，写出 $Y$ 的所有可能值，并估计 $Y$ 大于零的概率．

设数列 $\left\{a_n\right\}$ 满足 $a_1+3a_2+\dots +(2n-1)a_n=2n$ .

（1）求 $\left\{a_n\right\}$ 的通项公式；

（2）求数列 $\left\{\frac{a_n}{2_n+1}\right\}$ 的前 $n$ 项和.