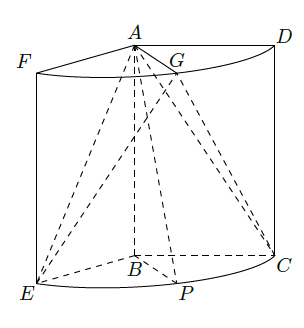
如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是 的中点．
（Ⅰ）设P是 上的一点，且 ，求 的大小；
（Ⅱ）当 ， 时，求二面角 的大小．
相关试题
，若
，求实数
的值。
所围成的平面图形的面积.
的展开式的各项系数之和等于
展开式中的常数项，求
的项的二项式系数.
在
上为增函数，求正实数
的取值范围；
时，求
上的最大值和最小值；
过椭圆E:
的右焦点
，且与E相交于
两点.
（
为原点），求点
的轨迹方程；
，求
的值.
相关知识点
推荐套卷
如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是 的中点．
（Ⅰ）设P是 上的一点，且 ，求 的大小；
（Ⅱ）当 ， 时，求二面角 的大小．
粤公网安备 44130202000953号