高中数学直线与平面的位置关系试题

已知平面 $\alpha$ 、 $\beta$ 、 $\gamma$ 两两垂直，直线 $a$ 、 $b$ 、 $c$ 满足： $a\subseteq \alpha$ ， $b\subseteq \beta$ ， $c\subseteq \gamma$ ，则直线 $a$ 、 $b$ 、 $c$ 不可能满足以下哪种关系（ ）

A．

两两垂直

B．

两两平行

C．

两两相交

D．

两两异面

如图， $\mathit{AE}\perp$平面 $\mathit{ABCD}$， $\mathit{CF}\parallel \mathit{AE},\mathit{AD}\parallel \mathit{BC}$， $\mathit{AD}\perp \mathit{AB},\mathit{AB}=\mathit{AD}=1,\mathit{AE}=\mathit{BC}=2$．

（Ⅰ）求证： $\mathit{BF}\parallel$平面 $\mathit{ADE}$；

（Ⅱ）求直线 $\mathit{CE}$与平面 $\mathit{BDE}$所成角的正弦值；

（Ⅲ）若二面角 $E-\mathit{BD}-F$的余弦值为 $\frac{1}{3}$，求线段 $\mathit{CF}$的长．

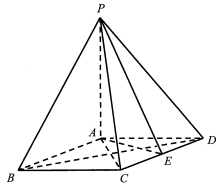
如图，在四棱锥 $P-\mathit{ABCD}$ 中， $\mathit{PA}\perp \mathrm{平面}ABCD$ ，底部 ABCD为菱形， E为 CD的中点．

（Ⅰ）求证： $\mathit{BD}\perp \mathrm{平面}PAC$ ；

（Ⅱ）若 $\angle \mathit{ABC}=60°$ ，求证： $\mathit{平面}\mathit{PAB}\perp \mathit{平面}\mathit{PAE}$ ；

（Ⅲ）棱 PB上是否存在点 F，使得 $\mathit{CF}\parallel \mathit{平面}\mathit{PAE}$ ？说明理由．

已知 l， m是平面 $\alpha$ 外的两条不同直线．给出下列三个论断：

① $l\perp m$ ；

② $m\parallel \alpha$ ；

③ $l\perp \alpha$ ．

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．

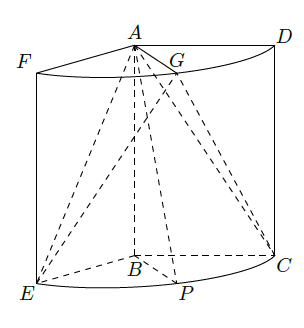
如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是 $\widehat{\mathit{DF}}$ 的中点．

（Ⅰ）设P是 $\widehat{\mathit{CE}}$ 上的一点，且 $\mathit{AP}\perp \mathit{BE}$ ，求 $\angle \mathit{CBP}$ 的大小；

（Ⅱ）当 $\mathit{AB}=3$ ， $\mathit{AD}=2$ 时，求二面角 $E﹣\mathit{AG}﹣C$ 的大小．

在正方体 $\mathit{ABCD}-A_1{B}_1{C}_1{D}_1$ 中， E为棱 CD的中点，则（ ）

A．

$A_{1}E\perp D{C}_1$

B．

$A_{1}E\perp \mathit{BD}$

C．

$A_{1}E\perp B{C}_1$

D．

$A_{1}E\perp \mathit{AC}$

如图，在直三棱柱ABC－A ₁B ₁C ₁中，D ， E分别为BC ， AC的中点，AB=BC ．

求证：

（1） A ₁ B ₁∥平面 DEC ₁；

（2） BE⊥ C ₁ E．