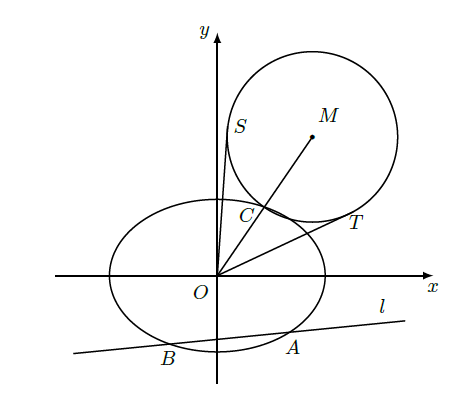在平面直角坐标系 中,椭圆 的离心率为 ,焦距为2.
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为 , 且看 ,M是线段OC延长线上一点,且 ,⊙M的半径为 ,OS,OT是⊙M的两条切线,切点分别为S,T,求 的最大值,并求取得最大值时直线l的斜率.
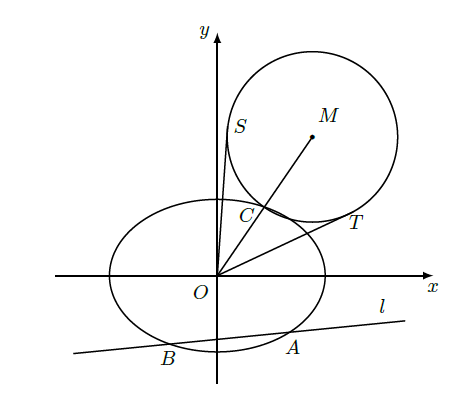
推荐套卷
在平面直角坐标系 中,椭圆 的离心率为 ,焦距为2.
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为 , 且看 ,M是线段OC延长线上一点,且 ,⊙M的半径为 ,OS,OT是⊙M的两条切线,切点分别为S,T,求 的最大值,并求取得最大值时直线l的斜率.