高中数学解答题

（本小题满分16分）某仓库为了保持库内温度，四周墙上装有如图所示的通风设施，该设施的下部是等边三角形ABC，其中AB=2米，上部是半圆，点E为AB的中点．△EMN是通风窗，（其余部分不通风）MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆（MN和AB不重合）．

（1）设MN与C之间的距离为x米，试将△EMN的面积S表示成的函数；
（2）当MN与C之间的距离为多少时，△EMN面积最大？并求出最大值．

甲、乙两所学校高三年级分别有1 200人，1 000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：

分组	[70,80）	[80,90）	[90,100）	[100,110）
频数	3	4	8	15
分组	[110,120）	[120,130）	[130,140）	[140,150]
频数	15	x	3	2

 
乙校：

分组	[70,80）	[80,90）	[90,100）	[100,110）
频数	1	2	8	9
分组	[110,120）	[120,130）	[130,140）	[140,150]
频数	10	10	y	3

 
（1）计算x，y的值；
（2）若规定考试成绩在[120, 150]内为优秀，请分别估计两所学校数学成绩的优秀率；
（3）由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0．10的前提下
认为两所学校的数学成绩有差异．

	甲校	乙校	总计
优秀
非优秀
总计

 
参考数据与公式：
临界值表

P（K^2≥k0）	0．10	0．05	0．010
k0	2．706	3．841	6．635

 

（本小题满分12分）已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．

（Ⅰ）若M为CB中点，证明：；
（Ⅱ）求这个几何体的体积．

已知，
（1）求函数 （）的单调递增区间；
（2）设的内角满足，而，求边上的高长的最大值。

设函数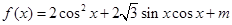
（1）求函数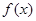的最小正周期和单调递减区间;
（2）若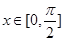，是否存在实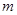数，使函数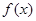的值域恰为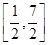？若存在，请求出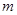的值，若不存在，请说明理由．

已知等差数列{a_n}的首项a₁＝1，公差d>0，且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项．
（1）求数列{a_n}的通项公式；
（2）设b_n＝ （n∈N^*），S_n＝b₁＋b₂＋…＋b_n，是否存在最大的整数t，使得对任意的n均有S_n>总成立？若存在，求出t；若不存在，请说明理由．

（本题12分）已知函数．
（1）求的值；
（2）数列满足求证：数列是等差数列
（3），试比较与的大小．

如图，A，B，C是椭圆M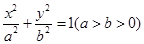：上的三点，其中点A是椭圆的右顶点，BC过椭圆M的中心，且满足AC⊥BC，BC＝2AC。

（1）求椭圆的离心率；
（2）若y轴被△ABC的外接圆所截得弦长为9，求椭圆方程。

已知函数，
（1）若，求在区间上的最小值；
（2）若在区间上有最大值3，求实数的值．

设函数，曲线在点处的切线斜率为0．
（1）求；
（2）若存在使得，求的取值范围。

（本小题13分）已知不等式的解集是．
（1）求，的值；          
（2）解不等式（为常数） ．

（满分12分）已知点F为抛物线的焦点，点P时准线上的动点，直线PF交抛物线C于A、B两点，若点P的纵坐标为，点D为准线与轴的交点。

（Ⅰ）求直线PF的方程；
（Ⅱ）求△DAB的面积S的范围；
（Ⅲ）设，，求证为定值。

（本小题满分12分）设m∈R，在平面直角坐标系中，已知向量a＝（mx，y+1），向量b=（x，y-1），，动点M（x，y）的轨迹为E．
（1）求轨迹E的方程，并说明该方程所表示曲线的形状;
（2）已知，证明：存在圆心在原点的圆，使得该圆的任意一条切线与轨迹E恒有两个交点A，B，且OA⊥OB（O为坐标原点），并求该圆的方程。

（本小题满分12分）已知函数，．
（Ⅰ）若，且存在单调递减区间，求的取值范围；
（Ⅱ）设函数的图象与函数的图象交于点、，过线段的中点作轴的垂线分别交、于点、，是否存在点，使在点处的切线与在点处的切线平行？如果存在，求出点的横坐标，如果不存在，说明理由．

（本小题满分12分）如图，在三棱柱中，面为矩形，，，为的中点，与交于点，面．

（Ⅰ）证明：；
（Ⅱ）若，求二面角的余弦值．