(本小题满分12分)我们把一系列向量 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作 ,已知向量列
,已知向量列 满足:
满足: ,
,
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 表示向量
表示向量 与
与 间的夹角,若
间的夹角,若 ,对于任意正整数
,对于任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的范围
的范围
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
甲、乙两地相距1000 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的 倍,固定成本为
倍,固定成本为 元.
元.
(Ⅰ)将全程运输成本 (元)表示为速度
(元)表示为速度 (
( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(Ⅱ)为了使全程运输成本最小,货车应以多大的速度行驶?
(本小题满分14分)平面内一动点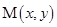 到定点
到定点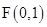 和到定直线
和到定直线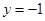 的距离相等,设
的距离相等,设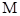 的轨迹是曲线
的轨迹是曲线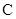 .
.
(1)求曲线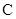 的方程;
的方程;
(2)在曲线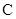 上找一点
上找一点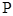 ,使得点
,使得点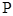 到直线
到直线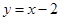 的距离最短,求出
的距离最短,求出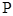 点的坐标;
点的坐标;
(3)设直线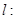
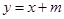 ,问当实数
,问当实数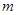 为何值时,直线
为何值时,直线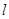 与曲线
与曲线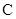 有交点?
有交点?
(本小题满分12分)已知 ,其中
,其中 均为实数,
均为实数,
(Ⅰ)求 的极值;
的极值;
(Ⅱ)设 ,
,
求证:对 恒成立;
恒成立;
(Ⅲ)设 ,若对
,若对 给定的
给定的 ,在区间
,在区间 上总存在
上总存在 使得
使得 成立,求m的取值范围.
成立,求m的取值范围.
(本小题满分12分)已知向量 ,
, ,函数
,函数 ,
, .
.
(Ⅰ)求函数 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)将函数 图像向下平移
图像向下平移 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 的解析式并作出它在
的解析式并作出它在 上的图像.
上的图像.
曲线C上任一点到定点(0, )的距离等于它到定直线
)的距离等于它到定直线 的距离.
的距离.
(1)求曲线C的方程;
(2)经过P(1,2)作两条不与坐标轴垂直的直线
 分别交曲线C于A、B两点,且
分别交曲线C于A、B两点,且 ⊥
⊥ ,设
,设 是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
(本小题满分12分)已知函数 以
以 为切点的切线方程是
为切点的切线方程是 .
.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)求函数 切线倾斜角
切线倾斜角 的取值范围.
的取值范围.
已知偶函数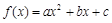 (
( )在点
)在点 处的切线与直线
处的切线与直线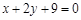 垂直,函数
垂直,函数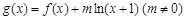 .
.
(Ⅰ)求函数 的解析式.
的解析式.
(Ⅱ)当 时,求函数
时,求函数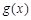 的单调区间和极值点;
的单调区间和极值点;
(Ⅲ)证明:对于任意实数x,不等式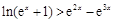 恒成立.(其中e=2.71828…是自然对数的底数)
恒成立.(其中e=2.71828…是自然对数的底数)
(本小题满分10分)已知 (
( ),
), ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
.
(1)当 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2)求证:当 时,
时, ;
;
(3)是否存在实数 ,使
,使 的最小值是
的最小值是 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)已知a>0,函数f(x)=-2asin ,当x∈
,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)求f(x)的单调区间;
(3)指出所求函数图像是由f(x)=sinx的图像如何变换得到的.
(本小题满分15分)如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.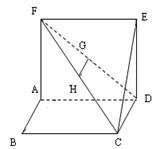
(1)求证: 平面
平面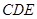 ;
;
(2)求证: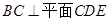 ;
;
(3)求三棱锥 的体积.
的体积.