甲、乙两地相距1000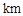
，货车从甲地匀速行驶到乙地，速度不得超过80
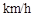，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的
倍，固定成本为
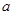元．
（Ⅰ）将全程运输成本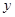
（元）表示为速度
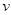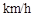（）的函数，并指出这个函数的定义域；
（Ⅱ）为了使全程运输成本最小，货车应以多大的速度行驶？
相关试题
中，
分别为内角
的对边，满足
．
，试求内角B、C的大小．
．
的最小值；
，命题
：关于
的不等式
对任意
：函数
是增函数．若“
的取值范围．
=
(
).
在点
处的切线与圆
相切,求
的值;
在
上恒成立？如果存在，试实数
=
.
=
在[-2,
]恰有2解，求实数
的取值范围.
}是等差数列，
=4，其前10项和
=100，数列{
}满足
.
，求数列{
}的前n项和
．推荐套卷
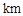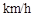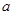甲、乙两地相距1000，货车从甲地匀速行驶到乙地，速度不得超过80，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的倍，固定成本为元．
（Ⅰ）将全程运输成本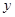（元）表示为速度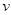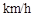（）的函数，并指出这个函数的定义域；
（Ⅱ）为了使全程运输成本最小，货车应以多大的速度行驶？
粤公网安备 44130202000953号