如图, 已知底角为 的等腰梯形
的等腰梯形 , 底边
, 底边 长为
长为 , 腰长为
, 腰长为 , 当一条垂直于底边
, 当一条垂直于底边 的直线
的直线 从左至右移动(与梯形
从左至右移动(与梯形 有公共点)时, 直线
有公共点)时, 直线 把梯形分成两部分, 令
把梯形分成两部分, 令 , 试写出左边部分的面积
, 试写出左边部分的面积 与
与 的函数解析式, 并画出大致图象.
的函数解析式, 并画出大致图象.
(本小题满分8分)
已知函数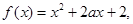
(1)求实数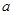 的取值范围,使函数
的取值范围,使函数 在区间
在区间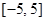 上是单调函数;
上是单调函数;
(2)若 , 记
, 记 的最大值为
的最大值为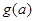 , 求
, 求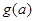 的表达式并判断其奇偶性.
的表达式并判断其奇偶性.
某饮料公司对一名员工进行测试以便确定其考评级别,公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,
现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
已知椭圆C的中心为直角坐标系xOy的原点,焦点在x轴上,它的一个顶点到两个焦点的距离分别是7和1
(1)求椭圆C的方程;
(2)若P为椭圆C的动点,M为过P且垂直于x轴的直线上的点, ,e为椭圆C的离心率,求点M的轨迹方程,并说明轨迹是什么曲线.
,e为椭圆C的离心率,求点M的轨迹方程,并说明轨迹是什么曲线.