(本小题满分14分)设函数 ,
, 且
且 . 曲线
. 曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 .
.
(1)求 的值;
的值;
(2)若存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
已知函数f(x)=x3+ax2+bx+a2(a,b∈R).
(1)若函数f(x)在x=1处有极值10,求b的值;
(2)若对于任意的a∈[-4,+∞),f(x)在x∈[0,2]上单调递增,求b的最小值.
已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中a∈R.
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)当a≠ 时,求函数y=f(x)的单调区间与极值.
时,求函数y=f(x)的单调区间与极值.
在平面直角坐标系 中,已知P是函数
中,已知P是函数 (x>0)的图象上的动点,该图象在点P处的切线
(x>0)的图象上的动点,该图象在点P处的切线 交y轴于点M,过点P作
交y轴于点M,过点P作 的垂线交y轴于点N,设线段MN的中点的纵坐标为
的垂线交y轴于点N,设线段MN的中点的纵坐标为 ,则
,则 的最大值是________.
的最大值是________.
设函数f(x)=ax2+bx+c(a,b,c∈R).若x=-1为函数f(x)ex的一个极值点,则下列图像不可能为y=f(x)图像的是________.(填写序号)
已知函数f(x)=ax2-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围.
若直线 与曲线C满足下列两个条件:(i)直线
与曲线C满足下列两个条件:(i)直线 在点
在点 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点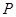 附近位于直线
附近位于直线 的两侧,则称直线
的两侧,则称直线 在点
在点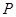 处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
①直线 在点
在点 入“切过”曲线
入“切过”曲线
②直线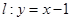 在点
在点 处“切过”曲线
处“切过”曲线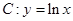
③直线 在点
在点 处“切过”曲线
处“切过”曲线
④直线 在点
在点 处“切过”曲线
处“切过”曲线
【改编】设曲线 在点
在点 处的切线方程为
处的切线方程为 ,则
,则 的值依次为( )
的值依次为( )
A. |
B. |
C. |
D. |
下列关于函数 的性质叙述错误的是( )
的性质叙述错误的是( )
A. 在区间 在区间 上单调递减 上单调递减 |
B. 在定义域上没有最大值 在定义域上没有最大值 |
C. 在 在 处取最大值3 处取最大值3 |
D. 的图像在点 的图像在点 处的切线方程为 处的切线方程为 |
已知函数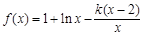 ,其中
,其中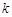 为常数.
为常数.
(1)若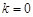 ,求曲线
,求曲线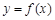 在点
在点 处的切线方程;
处的切线方程;
(2)若 ,求证:
,求证: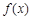 有且仅有两个零点;
有且仅有两个零点;
(3)若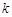 为整数,且当
为整数,且当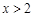 时,
时,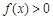 恒成立,求
恒成立,求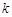 的最大值.
的最大值.
已知曲线 在
在 处的切线方程是
处的切线方程是 .
.
(1)求 的解析式;
的解析式;
(2)求曲线过点 的切线方程.
的切线方程.