高中数学组合几何试题

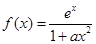已知函数，其中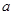为实数，常数.
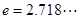(1) 若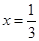是函数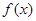的一个极值点，求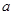的值；
(2) 当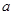取正实数时，求函数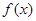的单调区间；
(3) 当时，直接写出函数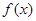的所有减区间.

函数的图像在点）处的切线与轴的交点的横坐标为（）若，则=               。

若曲线在点处的切线平行于轴,则 

A．

B．0

C．1

D．2

直线与曲线相切，则切点的坐标为       ．.

是否存在实数a，使函数f(x)＝log_a(ax²－x)在区间[2,4]上是增函数？如果存在，求出a的取值范围；如果不存在，请说明理由．

已知直线l过点，且与曲线相切，则直线的方程为              ．

已知函数，点．
（1）若，函数在上既能取到极大值，又能取到极小值，求的取值范围；
（2）当时，对任意的恒成立，求的取值范围；
（3）若，函数在和处取得极值，且，是坐标原点，证明：直线与直线不可能垂直.

函数f（x）在定义域R内可导，若f（x）＝f（2－x），且（x－1）f ′（x）>0，a＝f（0），b＝f（），c＝f（3），则a，b，c的大小关系是

A．a>b>c

B．c>a>b

C．b>a>c

D．c>b>a

过曲线C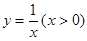：上一点作曲线C的切线，若切线的斜率为－4，则等于（   ）

A．2

B．

C．4

D．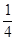

曲线在点（1，3）处的切线方程为         ．

若直线是曲线的切线，则的值为           .

若曲线在点处的切线与两坐标轴围成的三角形面积为18.则(   )

A．64

B．32

C．16

D．8

已知是上的可导函数，满足（）恒成立，，若曲线在点处的切线为，且，则等于（  ）

A．

B．

C．

D．

曲线y=e^2x在点（0，1）处的切线方程为（　　）.

A．y=x+1

B．y=﹣2x+1

C．y=2x﹣1

D．y=2x+1

曲线y=e^2x在点（0，1）处的切线方程为（ ）.

A．y=x+1

B．y=﹣2x+1

C．y=2x﹣1

D．y=2x+1