辽宁省鞍山市高二下学期期末考试理科数学试卷
从甲地去乙地有3班火车,从乙地去丙地有2班轮船,甲到丙地再无其他路可走,则从甲地去丙地可选择的旅行方式有
| A.5种 | B.6种 | C.7种 | D.8种 |
用反证法证明命题:“若a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为
| A.a,b都能被3整除 | B.a,b都不能被3整除 |
| C.a,b不都能被3整除 | D.a不能被3整除 |
设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(-1<X<0)等于
A.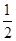 p p |
B.1-p | C.1-2p | D.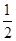 -p -p |
 展开式中只有第六项的二项式系数最大,则展开式的常数项是
展开式中只有第六项的二项式系数最大,则展开式的常数项是
| A.360 | B.180 | C.90 | D.45 |
设随机变量X~B(n,p),且E(X)=1.6,D(X)=1.28,则
| A.n=8,p=0.2 | B.n=4,p=0.4 | C.n=5,p=.32 | D.n=7,p=0.45 |
将三颗骰子各掷一次,设事件A为“三个点数都不相同”,事件B为“至少出现一个6点”,则概率P(A|B)的值为
A. B.
B. C.
C. D.
D.
函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图象如下图所示,则函数f(x)在开区间(a,b)内有极大值点
| A.1个 | B.2个 | C.3个 | D.4个 |
若q<19,则将(x-q)(x-q-1)(x-q-2) (x-19)写成 的形式是
的形式是
A. |
B. |
C. |
D. |
设△ABC的三边长分别为a,b,c,△ABC的面积为S,内切圆半径为r,则r= ,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
A. |
B. |
C. |
D. |
函数f(x)在定义域R内可导,若f(x)=f(2-x),且(x-1)f ′(x)>0,a=f(0),b=f( ),c=f(3),则a,b,c的大小关系是
),c=f(3),则a,b,c的大小关系是
| A.a>b>c | B.c>a>b | C.b>a>c | D.c>b>a |
若由一个2×2列联表中的数据计算得χ2=4.073,那么有 的把握认为两变量有关系(已知P(χ2≥3.841)≈0.05,P(χ2≥5.024)≈0.025).
今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 种不同的方法.(用数字作答)
若多项式x2+x10=a0+a1(x+1)+ +a9(x+1)9+a10(x+1)10,则a9= .
变速直线运动的物体的速度为v(t)=1-t 2(m/s)(其中t为时间,单位:s),则它在前2 s内所走过的路程为 m.
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
(可能用到的公式: ,
, ,其中
,其中 、
、 是对回归直线方程
是对回归直线方程 中系数
中系数 、
、 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
在数列{an}中,a1= ,an+1=
,an+1= ,求a2、a3、a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
,求a2、a3、a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
甲、乙两名跳高运动员一次试跳2米高度成功的概率分别为0.7、0.6,且每次试跳成功与否相互之间没有影响,求:
(1)甲试跳三次,第三次才成功地概率;
(2)甲、乙两人在第一次试跳中至少有一人成功的概率;
(3)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
已知函数 .
.
(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间.
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使 .
.
(1)求证:E、D、G、O四点共圆;
(2)如果CB=OB,试求 的值.
的值.
如图,已知⊙ 与⊙
与⊙ 相交于
相交于 、
、 两点,过点A作⊙
两点,过点A作⊙ 的切线交⊙O2于点
的切线交⊙O2于点 ,过点
,过点 作两圆的割线,分别交⊙
作两圆的割线,分别交⊙ 、⊙
、⊙ 于点
于点 、
、 ,
, 与
与 相交于点
相交于点 .[来源
.[来源
(1)求证: ;
;
(2)若 是⊙
是⊙ 的切线,且
的切线,且 ,
, ,求
,求 的长.
的长.
在直角坐标系 中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1
中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1
的极坐标方程为 ,曲线C2的直角坐标方程为
,曲线C2的直角坐标方程为 .
.
(1)求曲线C1的直角坐标方程;
(2)已知 为曲线C2上一点,Q为曲线C1上一点,求P、Q两点间距离的最小值.
为曲线C2上一点,Q为曲线C1上一点,求P、Q两点间距离的最小值.
已知圆 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)将圆 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆 ,
, 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
 是虚数单位,复数
是虚数单位,复数 的共轭复数是
的共轭复数是

 .
. 时,
时, ≤3,求
≤3,求 的取值范围;
的取值范围; ,
, 恒成立,求实数
恒成立,求实数 +
+ ≤2.
≤2. 粤公网安备 44130202000953号
粤公网安备 44130202000953号