某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告费支出为10百万元时，销售额多大？
（可能用到的公式：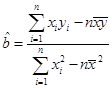
，
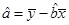，其中
、
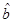是对回归直线方程
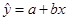中系数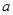
、
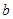按最小二乘法求得的估计值）
相关试题
前n项和为
，且
满足
且
（n≥1），求数列
，其中向量
，
，
，
的最大值和最小正周期；
上的单增区间。
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
，且满足
。
的坐标； (2)求向量
的夹角。
．相关知识点
推荐套卷
粤公网安备 44130202000953号