已知函数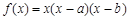 ,点
,点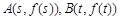 .
.
(1)若 ,函数
,函数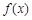 在
在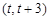 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求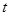 的取值范围;
的取值范围;
(2)当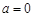 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求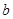 的取值范围;
的取值范围;
(3)若 ,函数
,函数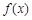 在
在 和
和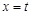 处取得极值,且
处取得极值,且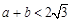 ,
,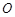 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
相关知识点
推荐套卷
已知函数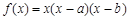 ,点
,点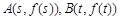 .
.
(1)若 ,函数
,函数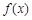 在
在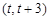 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求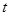 的取值范围;
的取值范围;
(2)当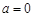 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求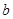 的取值范围;
的取值范围;
(3)若 ,函数
,函数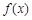 在
在 和
和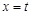 处取得极值,且
处取得极值,且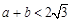 ,
, 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.