(本小题满分14分)已知直线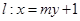 过椭圆
过椭圆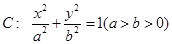 的右焦点
的右焦点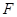 ,抛物线
,抛物线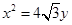 的焦点为椭圆
的焦点为椭圆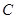 的上顶点,且直线
的上顶点,且直线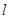 交椭圆
交椭圆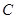 于
于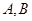 两点.
两点.
(1)求椭圆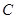 的方程;
的方程;
(2)若直线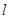 交
交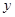 轴于点
轴于点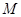 ,且
,且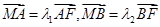 ,当
,当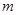 变化时,
变化时, 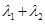 的值是否为定值?若是,求出这个定值,若不是,说明由.
的值是否为定值?若是,求出这个定值,若不是,说明由.
相关知识点
推荐套卷
(本小题满分14分)已知直线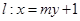 过椭圆
过椭圆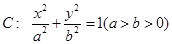 的右焦点
的右焦点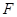 ,抛物线
,抛物线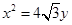 的焦点为椭圆
的焦点为椭圆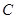 的上顶点,且直线
的上顶点,且直线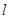 交椭圆
交椭圆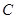 于
于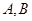 两点.
两点.
(1)求椭圆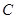 的方程;
的方程;
(2)若直线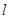 交
交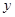 轴于点
轴于点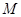 ,且
,且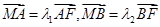 ,当
,当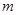 变化时,
变化时, 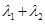 的值是否为定值?若是,求出这个定值,若不是,说明由.
的值是否为定值?若是,求出这个定值,若不是,说明由.