高中数学组合几何试题

若偶函数（x∈R且）在上的解析式为，则函数的图象在点处的切线的斜率为_________．

已知点A(1,1)和B(－1，－3)在曲线C：y＝ax³＋bx²＋d(a，b，d均为常数)上．若曲线C在点A，B处的切线互相平行，则a³＋b²＋d＝________.

函数的图像在点）处的切线与轴的交点的横坐标为（）若，则=               。

若曲线f(x)＝，g(x)＝x^α在点P(1,1)处的切线分别为l₁，l₂，且l₁⊥l₂，则实数α的值为(　　)

A．－2

B．2

C．

D．－

设点是曲线（为实常数）上任意一点，点处切线的倾斜角为，则的取值范围是（  ）

A．

B．

C．

D．

设函数，曲线在点处的切线方程为，则曲线在点处切线的斜率为（   ）

A．2

B．

C．

D．4

已知函数f(x)＝(x²＋ax－2a²＋3a)e^x(x∈R)，其中a∈R.
(1)当a＝0时，求曲线y＝f(x)在点(1，f(1))处的切线的斜率；
(2)当a≠时，求函数y＝f(x)的单调区间与极值．

【原创】设曲线在原点处切线与直线垂直，则        

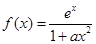已知函数，其中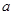为实数，常数.
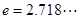(1) 若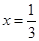是函数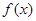的一个极值点，求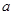的值；
(2) 当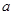取正实数时，求函数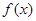的单调区间；
(3) 当时，直接写出函数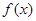的所有减区间.

当a>0时，函数f(x)＝(x²－2ax)e^x的图象大致是(　　)

已知函数f(x)＝x³＋ax²＋bx＋a²(a，b∈R)．
(1)若函数f(x)在x＝1处有极值10，求b的值；
(2)若对于任意的a∈[－4，＋∞)，f(x)在x∈[0,2]上单调递增，求b的最小值．

若曲线在点处的切线平行于轴,则 

A．

B．0

C．1

D．2

直线与曲线相切，则切点的坐标为       ．.

记定义在R上的函数y＝f(x)的导函数为f′(x)．如果存在x₀∈[a，b]，使得f(b)－f(a)＝f′(x₀)(b－a)成立，则称x₀为函数f(x)在区间[a，b]上的“中值点”．那么函数f(x)＝x³－3x在区间[－2,2]上“中值点”的个数为________．

已知函数f(x)＝ax²－(a＋2)x＋lnx.
(1)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；
(2)当a>0时，若f(x)在区间[1，e]上的最小值为－2，求a的取值范围．