高考数学（理）一轮配套特训：2-12导数的应用二

函数y＝x⁴－4x＋3在区间[－2,3]上的最小值为(　　)

函数f(x)＝x²－2ax＋a在区间(－∞，1)上有最小值，则函数g(x)＝在区间(1，＋∞)上一定(　　)

若函数f(x)＝x³－3x在(a,6－a²)上有最小值，则实数a的取值范围是(　　)

A．(－，1)	B．[－，1)
C．[－2,1)	D．(－2,1)

函数f(x)＝e^x(sinx＋cosx)在区间[0，]上的值域为(　　)

设f′(x)是函数f(x)的导函数，将y＝f(x)和y＝f′(x)的图象画在同一个直角坐标系中，不可能正确的是(　　)

已知函数f(x)是定义在(－∞，0)∪(0，＋∞)上的偶函数，当x>0时，f(x)＝lnx－ax，若函数在定义域上有且仅有4个零点，则实数a的取值范围是(　　)

A．(e，＋∞)	B．(0，)
C．(1，)	D．(－∞，)

函数f(x)＝－x³＋mx²＋1(m≠0)在(0,2)内的极大值为最大值，则m的取值范围是________．

已知函数f(x)＝(x²－3x＋3)e^x，设t>－2，函数f(x)在[－2，t]上为单调函数时，t的取值范围是________．

设直线x＝t与函数f(x)＝x²，g(x)＝lnx的图象分别交于点M，N，则当|MN|达到最小时t的值为________．

已知函数f(x)＝x³＋ax²＋bx＋a²(a，b∈R)．
(1)若函数f(x)在x＝1处有极值10，求b的值；
(2)若对于任意的a∈[－4，＋∞)，f(x)在x∈[0,2]上单调递增，求b的最小值．

已知函数f(x)＝(ax＋1)e^x.
(1)求函数f(x)的单调区间；
(2)当a>0时，求函数f(x)在区间[－2,0]上的最小值．

已知函数f(x)＝ax²－(a＋2)x＋lnx.
(1)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；
(2)当a>0时，若f(x)在区间[1，e]上的最小值为－2，求a的取值范围．

已知函数f(x)＝1＋x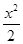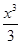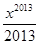－＋－＋…＋，则下列结论正确的是(　　)

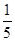已知函数y＝f(x)是定义在R上的奇函数，且当x>0时，f(x)＋xf′(x)>0(其中f′(x)是f(x)的导函数)，设a＝(4)f(4)，b＝f()，c＝(lg)f(lg)，则a，b，c由大到小的关系是________．

某公司为一家制冷设备厂设计生产一种长方形薄板，其周长为4米，这种薄板须沿其对角线折叠后使用．如图所示，ABCD(AB>AD)为长方形薄板，沿AC折叠后，AB′交DC于点P.当△ADP的面积最大时最节能，凹多边形ACB′PD的面积最大时制冷效果最好．

(1)设AB＝x(米)，用x表示图中DP的长度，并写出x的取值范围；
(2)若要求最节能，应怎样设计薄板的长和宽？
(3)若要求制冷效果最好，应怎样设计薄板的长和宽？