已知函数,其中
,且曲线
在点
处的切线垂直于
.
(1)求的值;
(2)求函数的单调区间与极值.
已知函数 (其中
(其中 ,
, ),函数
),函数 的导函数为
的导函数为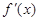 ,且
,且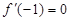 .
.
(Ⅰ)若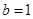 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求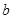 的值.
的值.
如图y=" f" (x)是可导函数,直线 : y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g
: y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g (x)是g(x)的导函数,则g
(x)是g(x)的导函数,则g (3)=( )
(3)=( )
| A.-1 | B.0 | C.2 | D.4 |
已知函数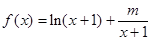 .
.
(1)当函数 在点
在点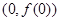 处的切线与直线
处的切线与直线 垂直时,求实数
垂直时,求实数 的值;
的值;
(2)若 时,
时,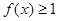 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数f(x)=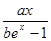 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+(e–1)2y–e=0.其中e =2.71828 为自然对数的底数.
,曲线y=f(x)在点(1,f(1))处的切线方程为x+(e–1)2y–e=0.其中e =2.71828 为自然对数的底数.
(Ⅰ)求a,b的值;
(Ⅱ)如果当x≠0时,f(2x)<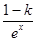 ,求实数k的取值范围.
,求实数k的取值范围.
点P是曲线x2-y-2ln =0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
=0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
A. (1-ln 2) (1-ln 2) |
B. (1+ln 2) (1+ln 2) |
C.  |
D. (1+ln 2) (1+ln 2) |
若直线 与曲线C满足下列两个条件:(i)直线
与曲线C满足下列两个条件:(i)直线 在点
在点 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点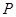 附近位于直线
附近位于直线 的两侧,则称直线
的两侧,则称直线 在点
在点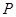 处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
①直线 在点
在点 入“切过”曲线
入“切过”曲线
②直线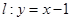 在点
在点 处“切过”曲线
处“切过”曲线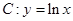
③直线 在点
在点 处“切过”曲线
处“切过”曲线
④直线 在点
在点 处“切过”曲线
处“切过”曲线