期中备考总动员高三理数学模拟卷【新课标2】2
下列命题中:
①命题“若 ,则
,则 或
或 ”的逆否命题为“若
”的逆否命题为“若 或
或 ,则
,则 ”.
”.
②命题p: “存在 R,使得
R,使得
 0”的否定是“任意
0”的否定是“任意 ,使得
,使得 >0”;
>0”;
③回归直线方程一定过样本中心点( ).其中真命题的个数为( )
).其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
【改编】设 为公差大于零的等差数列
为公差大于零的等差数列 的前
的前 项和,若
项和,若 ,则当
,则当 取到最小值时
取到最小值时 的值为( )
的值为( )
| A.3 | B.4 | C.5 | D.6 |
【原创题】设函数 (
( )的最大值为1,且其图象相邻两条对称轴的距离为
)的最大值为1,且其图象相邻两条对称轴的距离为 ,若将函数
,若将函数 的图象向右平移
的图象向右平移 个单位,所得图象对应函数为
个单位,所得图象对应函数为 ,则( )
,则( )
A. 的图象关于直线 的图象关于直线 对称, 对称, 图象关于原点对称 图象关于原点对称 |
B. 的图象关于点 的图象关于点 对称, 对称, 图象关于直线 图象关于直线 对称 对称 |
C. 的图象关于直线 的图象关于直线 对称, 对称, 图象关于原点对称 图象关于原点对称 |
D. 的图象关于点 的图象关于点 对称, 对称, 图象关于直线 图象关于直线 对称 对称 |
【原创题】两名男生和两名女生和数学老师拍照留念,求两名男生不相邻且两名女生不相邻的不同排法种数为_____.
【改编】已知 ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且 ,
, ,△ABC的面积为
,△ABC的面积为 ,三棱锥O-ABC的体积为
,三棱锥O-ABC的体积为 ,则球O的表面积为 .
,则球O的表面积为 .
(本小题满分12分)已知函数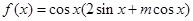 的图象经过点
的图象经过点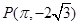 .
.
(Ⅰ)求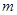 的值以及
的值以及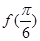 ;
;
(Ⅱ)函数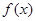 的图象向右平移
的图象向右平移 后得到函数
后得到函数 的图象,求
的图象,求 在
在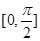 上的值域.
上的值域.
(本小题满分12分)如图,在四棱锥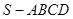 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, ,点
,点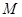 是
是 的中点,
的中点,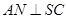 且交
且交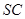 于点
于点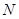 .
.
(Ⅰ)求证:平面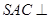 平面
平面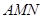 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设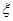 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求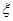 的分布列和数学期望.
的分布列和数学期望.
【改编题】(本小题满分12分)已知圆 ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若直线 (
( )与曲线
)与曲线 交于不同的两点
交于不同的两点 ,
, ,以线段
,以线段 为直径作圆
为直径作圆 .若圆
.若圆 与
与 轴相切,求直线
轴相切,求直线 被圆
被圆 所截得的弦长..
所截得的弦长..
选修4-1:几何证明选讲
如图,在 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 ,点
,点 是
是 边的中点,连接
边的中点,连接 交圆
交圆 于点
于点 .
.
(Ⅰ)求证: 是圆
是圆 的切线;
的切线;
(Ⅱ)求证: .
.
已知曲线 是动点
是动点 到两个定点
到两个定点 、
、 距离之比为
距离之比为 的点的轨迹。
的点的轨迹。
(1)求曲线 的方程;(2)求过点
的方程;(2)求过点 与曲线
与曲线 相切的直线方程。
相切的直线方程。
 ,集合
,集合 ,则
,则 ( )
( )



 ,
, ,若
,若 ,则
,则 ( )
( )



 ,且
,且 ,则
,则 等于( )
等于( )



 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( ) 时,则输出x的值为( )
时,则输出x的值为( )
 在点
在点 处的切线方程为
处的切线方程为 ,则
,则 的值依次为( )
的值依次为( )








 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 的值不可能是( )
的值不可能是( )



 的不等式
的不等式 对任意实数
对任意实数 的最大值为( )
的最大值为( )



 ,则
,则 的最大值为 .
的最大值为 . 中,已知
中,已知
 ,若
,若 分别是角
分别是角 所对的边,则
所对的边,则 的最小值为 .
的最小值为 . .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间. ,
, .
. 时,求不等式
时,求不等式 的解集;
的解集; ,且当
,且当 时,
时, ,求a的取值范围.
,求a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号