高中数学简单的等周问题解答题

已知命题p：函数y＝log_a(1－2x)在定义域上单调递增；命题q：不等式(a－2)x²＋2(a－2)x－4<0对任意实数x恒成立．若p∨q是真命题，求实数a的取值范围．

给定两个命题，：对任意实数都有恒成立；：．如果∨为真命题，∧为假命题，求实数的取值范围．

设命题p：函数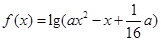的定义域为R；命题q：不等式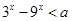对一切实数均成立。
（1）如果p是真命题，求实数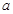的取值范围；
（2）如果命题“p或q”为真命题，且“p且q”为假命题，求实数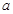的取值范围。

已知命题函数的值域为，命题方程在上有解，若命题“或”是假命题，求实数的取值范围.

已知，设命题P： ；命题Q：函数f（x）＝3x²＋2mx＋m＋有两个不同的零点．求使命题“P或Q”为真命题的实数的取值范围．

已知命题p：方程有两个不等的负实根，命题q：方程
无实根．若p或q为真，p且q为假，求实数的取值范围．

已知命题p：任意x∈R，x²＋1≥a都成立，命题q：方程表示双曲线．
（1）若命题p为真命题，求实数a的取值范围；
（2）若 “p且q”为真命题，求实数a的取值范围．

设命题函数是上的减函数，命题函数,的值域为，若“且”为假命题，“或”为真命题，求实数的取值范围．

已知,设命题函数的定义域为；命题当时,函数恒成立，如果为真命题,为假命题,求的取值范围．

(本小题满分10分)已知条件：和条件：，请选取适当的实数的值，分别利用所给的两个条件作为、构造命题“若则”，并使得构造的原命题为真命题，而其逆命题为假命题，则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题．

(本小题满分10分)已知命题p:函数在R上是减函数；命题q：在平面直角坐标系中，点在直线的左下方。若为假，为真，求实数的取值范围

本小题12分）已知命题p：方程表示焦点在y轴上的椭圆；命题q：双曲线的离心率，若p、q有且只有一个为真，求m的取值范围。

命题p： ，其中满足条件：五个数的平均数是20，标准差是； 命题q：m≤t≤n ，其中m,n满足条件：点M在椭圆上，定点A(1,0)，m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假，求实数t的取值范围。

命题P：函数内单调递减；命题Q：曲线轴交于不同的两点.
如果“P\/Q”为真且“P/\Q”为假，求a的取值范围.

（本小题满分12分）
设命题：方程表示焦点在坐标轴上的双曲线，命题：。
（1）写出命题的否定；
（2）若“或”为真命题，求实数的取值范围。