(本小题满分10分)已知条件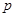
：
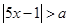和条件
：
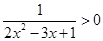，请选取适当的实数
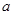的值，分别利用所给的两个条件作为
、
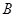构造命题“若则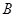”，并使得构造的原命题为真命题，而其逆命题为假命题，则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题．
在
和
处取得极值．
和
的值；
的单调区间相关知识点
推荐套卷
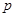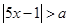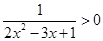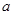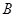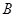(本小题满分10分)已知条件：和条件：，请选取适当的实数的值，分别利用所给的两个条件作为、构造命题“若则”，并使得构造的原命题为真命题，而其逆命题为假命题，则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题．
粤公网安备 44130202000953号