(本小题满分12分)
设同时满足条件:①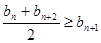 ;②
;②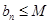 (
(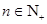 ,
,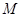 是与
是与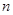 无关的常数)的无穷数列
无关的常数)的无穷数列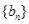 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列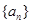 的前
的前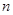 项和
项和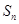 满足:
满足:
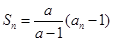 (
( 为常数,且
为常数,且 ,
,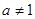 ).
).
(Ⅰ)求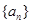 的通项公式;
的通项公式;
(Ⅱ)设 ,若数列
,若数列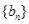 为等比数列,求
为等比数列,求 的值,并证明此时
的值,并证明此时 为“嘉文”数列.
为“嘉文”数列.
推荐套卷
(本小题满分12分)
设同时满足条件:①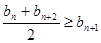 ;②
;②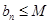 (
(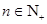 ,
,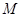 是与
是与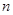 无关的常数)的无穷数列
无关的常数)的无穷数列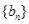 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列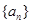 的前
的前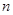 项和
项和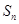 满足:
满足:
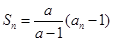 (
( 为常数,且
为常数,且 ,
,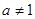 ).
).
(Ⅰ)求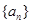 的通项公式;
的通项公式;
(Ⅱ)设 ,若数列
,若数列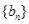 为等比数列,求
为等比数列,求 的值,并证明此时
的值,并证明此时 为“嘉文”数列.
为“嘉文”数列.