设 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从 中的任意一点
中的任意一点 作
作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
, ,记点
,记点 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为 .如果
.如果 是边长为1的正方形,那么
是边长为1的正方形,那么 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从 中的任意一点
中的任意一点 作
作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
, ,记点
,记点 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为 . 若
. 若 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
① 的最大值为
的最大值为 ;
;
② 的取值范围是
的取值范围是 ;
;
③ 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①② | D.①②③ |
设是正整数,
为正有理数.
(1)求函数的最小值;
(2)证明:;
(3)设,记
为不小于
的最小整数,例如
.令
的值.
(参考数据:.
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013,求
交点个数为2013,求 的值.
的值.
已知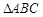 的三内角分别为
的三内角分别为 ,向量
,向量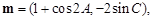
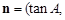
 ,记函数
,记函数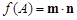 .
.
(1)若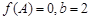 ,求
,求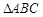 的面积;
的面积;
(2)若关于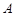 的方程
的方程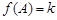 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
设函数 在区间
在区间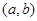 上的导函数为
上的导函数为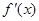 ,
,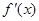 在区间
在区间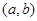 上的导函数为
上的导函数为 ,若在区间
,若在区间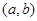 上
上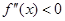 恒成立,则称函数
恒成立,则称函数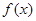 在区间
在区间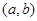 上为“凸函数”.已知
上为“凸函数”.已知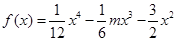 ,若对任意的实数
,若对任意的实数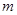 满足
满足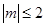 时,函数
时,函数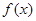 在区间上
在区间上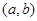 为“凸函数”,则
为“凸函数”,则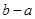 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |
已知函数 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
的零点的个数为( )
A.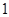 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
对实数a与b,定义新运算“⊗”: .设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A. |
B. |
C. |
D. |
没函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对一切实数x均成 立,则称
对一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:② :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |