湖南省高三十三校联考第二次考试理科数学试卷
已知 ,则“
,则“ ”是“复数
”是“复数 为虚数单位)为纯虚数”的( )
为虚数单位)为纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如图,给定由10个点(任意相邻两点距离为1)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )
| A.12 | B.13 |
| C.15 | D.16 |
若某棱锥的三视图(单位:cm)如图所示,则该棱锥的体积等于( )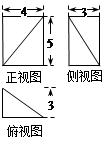
A.10cm3 B.20cm3 C.30cm3 B.40cm3
已知双曲线 ,
, 为实轴顶点,
为实轴顶点, 是右焦点,
是右焦点, 是虚轴端点,
是虚轴端点,
若在线段 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点 ,使得
,使得 构成以
构成以 为斜边的
为斜边的
直角三角形,则双曲线离心率 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),在以原点
为参数),在以原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .则
.则 与
与 的交点直角坐标为 .
的交点直角坐标为 .
给定有限单调递增数列 ,数列
,数列 至少有两项)且
至少有两项)且 ,定义集合
,定义集合 .若对任意点
.若对任意点 ,
,
存在点 使得
使得
 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(1)给出下列四个命题,其中正确的是 .(填上所有正确命题的序号)
①数列 -2,2具有性质
-2,2具有性质 ;
;
②数列 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质 ;
;
③若数列 具有性质
具有性质 ,则
,则 中一定存在两项
中一定存在两项 ,使得
,使得 ;
;
④若数列 具有性质
具有性质 ,
, 且
且 ,则
,则 .
.
(2)若数列 只有2014项且具有性质
只有2014项且具有性质 ,则
,则 的所有项和
的所有项和 .
.
已知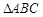 的三内角分别为
的三内角分别为 ,向量
,向量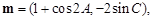
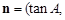
 ,记函数
,记函数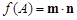 .
.
(1)若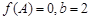 ,求
,求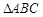 的面积;
的面积;
(2)若关于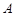 的方程
的方程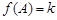 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
如图,在四棱锥 中,
中, 平面
平面 ,
, ,且
,且 ,点
,点 在
在 上.
上.
(1)求证: ;
;
(2)若二面角 的大小为
的大小为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,矩形 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点 在坐标原点
在坐标原点 分别为
分别为 轴、
轴、 轴,
轴, (百米),
(百米), (百米)(
(百米)( )观光区中间叶形阴影部分
)观光区中间叶形阴影部分 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段 相切(切点记为
相切(切点记为 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线 左下部分建设为花圃.记点
左下部分建设为花圃.记点 到
到 的距离为
的距离为 表示花圃的面积.
表示花圃的面积.
(1)求花圃面积 的表达式;
的表达式;
(2)求 的最小值.
的最小值.
已知 分别为椭圆
分别为椭圆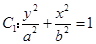 的上、下焦点,
的上、下焦点,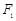 是抛物线
是抛物线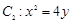 的焦点,点
的焦点,点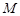 是
是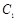 与
与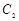 在第二象限的交点, 且
在第二象限的交点, 且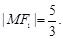
(1)求椭圆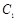 的方程;
的方程;
(2)与圆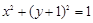 相切的直线
相切的直线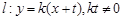 交椭
交椭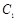 于
于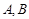 ,若椭圆
,若椭圆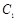 上一点
上一点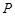 满足
满足 ,求实数
,求实数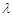 的取值范围.
的取值范围.
 ,
, 则
则 ( )
( )




 的前
的前 项和为
项和为 ,且
,且 ,则过 点
,则过 点 和
和 的直线的斜率是( )
的直线的斜率是( )
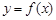 的图象如图,则函数
的图象如图,则函数 的图象大致为( )
的图象大致为( )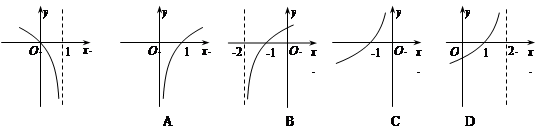
 在动直线
在动直线 上的射影为
上的射影为 ,点
,点 ,则
,则 的最大值是( )
的最大值是( )



 是
是 的重心,且
的重心,且 ,则实数
,则实数 的值为( )
的值为( )



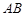 与
与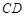 相交于点
相交于点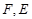 是
是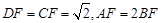 ,若
,若 与圆相切,且
与圆相切,且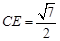 ,则
,则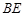 = .
= .
 ,则
,则 的最小值为 .
的最小值为 . 的值为 .
的值为 . 中,
中,
 是
是 的中点,
的中点, .
. 是
是 的中点,
的中点, 是
是 (包括边界)内任意一点,则
(包括边界)内任意一点,则 的取值范围是 .
的取值范围是 . 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 .
. 的取值范围;
的取值范围; 为自然对数的底数),求
为自然对数的底数),求 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号