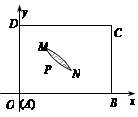如图,矩形 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点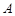 在坐标原点
在坐标原点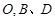 分别为
分别为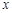 轴、
轴、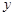 轴,
轴,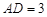 (百米),
(百米),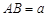 (百米)(
(百米)(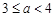 )观光区中间叶形阴影部分
)观光区中间叶形阴影部分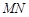 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数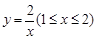 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段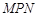 相切(切点记为
相切(切点记为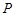 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线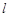 左下部分建设为花圃.记点
左下部分建设为花圃.记点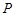 到
到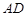 的距离为
的距离为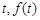 表示花圃的面积.
表示花圃的面积.
(1)求花圃面积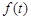 的表达式;
的表达式;
(2)求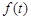 的最小值.
的最小值.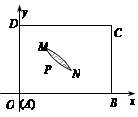
推荐套卷
如图,矩形 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点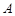 在坐标原点
在坐标原点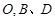 分别为
分别为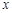 轴、
轴、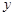 轴,
轴,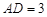 (百米),
(百米),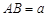 (百米)(
(百米)(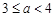 )观光区中间叶形阴影部分
)观光区中间叶形阴影部分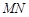 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数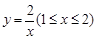 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段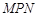 相切(切点记为
相切(切点记为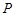 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线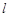 左下部分建设为花圃.记点
左下部分建设为花圃.记点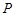 到
到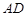 的距离为
的距离为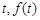 表示花圃的面积.
表示花圃的面积.
(1)求花圃面积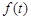 的表达式;
的表达式;
(2)求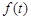 的最小值.
的最小值.