普通高等学校招生全国统一考试理科数学

在复平面内，复数$z=\frac{2i}{1+i}$（$i$为虚数单位）的共轭复数对应的点位于（）

已知全集为$R$，集合$A=\left\{\overline{)x}{\left(\frac{1}{2}\right)}^x⩽1\right\},B=\left\{\overline{)x}{x}^2-6x+8⩽0\right\}$，则$A\cap C_{R}B=$（）

在一次跳伞训练中，甲、乙两位学员各跳一次，设命题$p$是"甲降落在指定范围"，$q$是"乙降落在指定范围"，则命题"至少有一位学员没有降落在指定范围"可表示为（）

将函数$y=\sqrt{3}\cos x+\sin x(x\in R)$的图象向左平移$m(m>0)$个单位长度后，所得到的图象关于$y$轴对称，则$m$的最小值是（　　）

已知 $0<\theta <\frac{\pi }{4}$，则双曲线 $C_1:\frac{x^2}{{\cos }^2\theta }-\frac{y^2}{{\sin }^2\theta }=1与C_2:\frac{y^2}{{\sin }^2\theta }-\frac{x^2}{{\sin }^2\theta {\tan }^2\theta }=1$的（　　）

已知点$A(-1,1)$,$B(1,2)$,$C(-2,-1)$,$D(3,4）$，则向量$\stackrel{\rightharpoonup }{AB}$在$\stackrel{\rightharpoonup }{CD}$方向上的投影为

一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度$v\left(t\right)=7-3t+\frac{25}{1+t}(t$的单位：$s,v$的单位：$m/s$）行驶至停止，在此期间汽车继续行驶的距离（单位：$m$）是（）

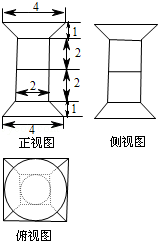
一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为$V_1,V_2,V_3,V_4$，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有（　　）

如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为$X$，则X的均值$E\left(X\right)=$.

已知 $a$为常数，函数 $f\left(x\right)=x(\ln x-ax)$有两个极值点 $x_1,x_2(x_1<x_2)$=（　　）

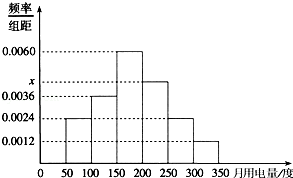
从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示：
（1）直方图中 $x$的值为；
（2）在这些用户中，用电量落在区间 $[100,250)$内的户数为．

阅读如图所示的程序框图，运行相应的程序，输出的结果 $i=$．

设$x,y,z\in R$，且满足：$x^2+y^2+z^2=1,x+2y+3z=\sqrt{14}$，则$x+y+z$=．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数 $1,3,6,10...$，第 $n$个三角形数为 $\frac{n(n+1)}{2}=\frac{1}{2}{n}^2+\frac{1}{2}n$．记第 $n$个 $k$边形数为 $N(n,k)$ $(k\ge 3)$，以下列出了部分 $k$边形数中第 $n$个数的表达式：
三角形数 $N(n,3)=\frac{1}{2}{n}^2+\frac{1}{2}n$，
正方形数 $N(n,4)=n^2$，
五边形数 $N(n,5)=\frac{3}{2}{n}^2-\frac{1}{2}n$，
六边形数 $N(n,6)=2n^2-n$，
…
可以推测 $N(n,k)$的表达式，由此计算 $N(10,24)=$．

如图，圆$O$上一点$C$在直径$AB$上的射影为$D$，点$D$在半径$OC$上的射影为$E$．若$AB=3AD$，则$\frac{CE}{EO}$的值为．

在直角坐标系$xOy$中，椭圆$C$的参数方程为$\left\{\begin{array}{l}x=a\cos \Phi \\ y=b\sin \Phi \end{array}\right.\left(\Phi \mathrm{为参数},a>b>0\right)$．在极坐标系（与直角坐标系$xOy$取相同的长度单位，且以原点$O$为极点，以$x$轴正半轴为极轴）中，直线$l$与圆$O$的极坐标方程分别为$\rho \sin \left(\theta +\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}m$（$m$为非零常数）与$\rho =b$．若直线$l$经过椭圆$C$的焦点，且与圆$O$相切，则椭圆$C$的离心率为

在$△ABC$中，角$A,B,C$对应的边分别是$a,b,c$，已知$\cos 2A-3\cos (B+C)=1$．
（1）求角$A$的大小；
（2）若$△ABC$的面积$S=5\sqrt{3},b=5$，求$\sin B\sin C$的值．

已知等比数列$\left\{a_n\right\}$满足：$\left|a_2-a_3\right|=10,a_1{a}_2{a}_3=125$．
（1）求数列$\left\{a_n\right\}$的通项公式；
（2）是否存在正整数$m$，使得$\frac{1}{a_1}+\frac{1}{a_2}+\cdots +\frac{1}{a_m}\ge 1$？若存在，求$m$的最小值；若不存在，说明理由．

如图， $AB$是圆 $O$的直径，点 $C$是圆 $O$上异于 $A,B$的点，直线 $PC\perp$平面 $ABC$， $E,F$分别是 $PA,PC$的中点．
（1）记平面 $BEF$与平面 $ABC$的交线为 $l$，试判断直线l与平面 $PAC$的位置关系，并加以证明；

（2）设（1）中的直线 $l$与圆 $O$的另一个交点为 $D$，且点 $Q$满足 $\stackrel{\to }{DQ}=\frac{1}{2}\stackrel{\to }{CP}$．记直线 $PQ$与平面 $ABC$所成的角为 $\theta$，异面直线与 $EF$所成的角为 $\alpha$，二面角 $E-l-C$的大小为 $\beta$．求证： $\sin \theta =\sin \alpha \sin \beta$．

假设每天从甲地去乙地的旅客人数$X$是服从正态分布$N$（800，50²）的随机变量．记一天中从甲地去乙地的旅客人数不超过900的概率为$p_0$．
（1）求$p_0$的值；
（参考数据：若$X~N(\mu ,{\sigma }^2)$，有$P(\mu -\sigma <X\le \mu +\sigma )=0.6826,P(\mu -2\sigma <X\le \mu +2\sigma )=0.9544$,$P(\mu -3\sigma <X\le \mu +3\sigma )=0.9974$．
（2）某客运公司用$A,B$两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次，$A,B$两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1600元/辆和2400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求$B$型车不多于$A$型车7辆．若每天要以不小于$p_0$的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备$A$型车、$B$型车各多少辆？

如图，已知椭圆$C_1$与$C_2$的中心在坐标原点$O$，长轴均为$MN$且在$x$轴上，短轴长分别为$2m,2n(m>n)$，过原点且不与$x$轴重合的直线l$l$与$C_1,C_2$的四个交点按纵坐标从大到小依次为$A,B,C,D$，记$\lambda =\frac{\pi }{n}$，$∆BDM$和$∆ABN$的面积分别为$S_1$和$S_2$．
（1）当直线$l与y$轴重合时，若$S_1=\lambda S_2$，求$\lambda$的值；
（2）当$\lambda$变化时，是否存在与坐标轴不重合的直线$l$，使得$S_1=\lambda S_2$？并说明理由．

设$n$是正整数，$r$为正有理数．
（1）求函数$f\left(x\right)={\left(1+x\right)}^{r+1}-\left(r+1\right)x-1\left(x>-1\right)$的最小值；
（2）证明：$\frac{n^{r+1}-{\left(n-1\right)}^{r+1}}{r+1}<n^r<\frac{{\left(n+1\right)}^{r+1}-n^{r+1}}{r+1}$；
（3）设$x\in R$，记$\left[x\right]$为不小于$x$的最小整数，例如$\left[2\right]=2,\left[\pi \right]=4,\left[-\frac{3}{2}\right]=-1$．令$S=\sqrt[3]{81}+\sqrt[3]{82}+\sqrt[3]{83}+\dots +\sqrt[3]{125}，求S$的值．
（参考数据：${80}^{\frac{4}{3}}\approx 344.7,{81}^{\frac{4}{3}}\approx 350.5，{124}^{\frac{4}{3}}\approx 618.3，{126}^{\frac{4}{3}}\approx 631.7$．