对于三次函数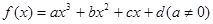 ,给出定义:设
,给出定义:设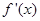 是函数
是函数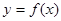 的导数,
的导数,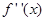 是
是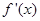 的导数,若方程
的导数,若方程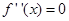 有实数解
有实数解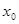 ,则称点
,则称点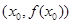 为函数
为函数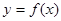 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数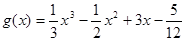 ,则
,则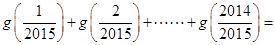 ( )
( )
| A.1 | B.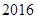 |
C.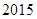 |
D.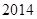 |
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“比增函数”;
为“比增函数”;
(Ⅰ)若函数 是“比增函数”,求实数
是“比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 为“比增函数”,且
为“比增函数”,且 的部分函数值由下表给出,
的部分函数值由下表给出,
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
求证: .
.
设函数 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,如果函数
上的两个函数,如果函数 在区间
在区间
上有 (
( )个不同的零点,那么称函数
)个不同的零点,那么称函数 和
和 在区间
在区间 上为“
上为“ 阶关联函数”.若
阶关联函数”.若 与
与 在
在 上是“
上是“ 阶关联函数”,则
阶关联函数”,则 的取值范围是()
的取值范围是()
A. |
B. |
C. |
D. |
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,仍是等比数列,则称
,仍是等比数列,则称 为“等比函数”.现有定义在
为“等比函数”.现有定义在 上的如下函数:①
上的如下函数:① ;②
;② ; ③
; ③ ; ④
; ④ .则其中是“等比函数”的
.则其中是“等比函数”的 的序号为.
的序号为.
若直角坐标平面内 两点满足条件:①点
两点满足条件:①点 都在
都在 的图象上;②点
的图象上;②点 关于原点对称,则对称点对
关于原点对称,则对称点对 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对 与
与 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数 , 则
, 则 的“兄弟点对”的个数为
的“兄弟点对”的个数为
| A.2 | B.3 | C.4 | D.5 |
(本小题满分14分)对于定义域为 的函数
的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间 ,使
,使 在
在 上的值域为
上的值域为 ;那么把
;那么把 (
( )叫闭函数,且条件②中的区间
)叫闭函数,且条件②中的区间 为
为 的一个“好区间”.
的一个“好区间”.
(1)求闭函数 的“好区间”;
的“好区间”;
(2)若 为闭函数
为闭函数 的“好区间”,求
的“好区间”,求 、
、 的值;
的值;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围.
的取值范围.
设m是一个非负整数,m的个位数记作 ,如
,如 ,
, ,
, ,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
① ;
;
② ,若
,若 ,都有
,都有 ;]
;]
③ ;
;
则正确的结论的个数为()
| A.3 | B.2 | C.1 | D.0 |
设m是一个非负整数,m的个位数记作 ,如
,如 ,
, ,
, ,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
① ;
;
② ,若
,若 ,都有
,都有 ;
;
③ ;
;
④ .
.
则正确的结论的个数为()
| A.1 | B.2 | C.3 | D.4 |
定义:如果函数 在定义域内给定区间
在定义域内给定区间 上存在
上存在
 ,满足
,满足 ,则称函数
,则称函数 是
是 上的“平均值函数”,
上的“平均值函数”, 是它的一个均值点,例如
是它的一个均值点,例如 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数 是
是 上的平均值函数,则实数
上的平均值函数,则实数 的取值范围是.
的取值范围是.
【原创】如果对定义在R上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 都有
都有 ,则称函数
,则称函数 为“M函数”.
为“M函数”.
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
以上函数是“M函数”的所有序号为__________(把所有正确命题的序号都填上).
对于函数 和
和 ,设
,设 ,
, ,若存在
,若存在 ,使得
,使得 ,则称
,则称 与
与 互为“零点相邻函数”.若函数
互为“零点相邻函数”.若函数 与
与 互为“零点相邻函数”,则实数
互为“零点相邻函数”,则实数 的取值范围是()
的取值范围是()
A. |
B. |
C. |
D. |
已知 是
是 内的一点(不含边界),且
内的一点(不含边界),且
 ,若
,若 的面积分别为
的面积分别为 ,记
,记 ,则
,则 的最小值为
的最小值为
A. |
B. |
C. |
D. |