对于自然数数组 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 的极差
的极差 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 实施操作
实施操作 ,…,实施
,…,实施 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
, .
.
(1)若 ,求
,求 和
和 的值;
的值;
(2)已知 的极差为
的极差为 且
且 ,若
,若 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值;
(3)若 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在 满足
满足 .
.
某种汽车购买时费用为 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增.
(1)设使用 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
设正项数列{an}的前n项和为Sn,若{an}和{ }都是等差数列,且公差相等.
}都是等差数列,且公差相等.
(1)求{an}的通项公式;
(2)若a1,a2,a5恰为等比数列{bn}的前三项,记数列cn= ,数列{cn}的前n项和为Tn.求证:对任意n∈N*,都有Tn<2.
,数列{cn}的前n项和为Tn.求证:对任意n∈N*,都有Tn<2.
已知数列{an}的通项公式是an=2n-3( )n,则其前20项和为( )
)n,则其前20项和为( )
A.380- (1- (1- ) ) |
B.400- (1- (1- ) ) |
C.420- (1- (1- ) ) |
D.440- (1- (1- ) ) |
对于各项均为整数的数列 ,如果
,如果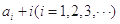 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:①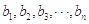 是
是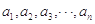 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列:
①数列1,2,3,4,5; ②数列1,2,3, ,11,12; ③数列 的前n项和为
的前n项和为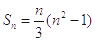 .
.
其中具有“P性质”或“变换P性质”的有( )
| A.③ | B.①③ | C.①② | D.①②③ |
对于正项数列 ,定义
,定义 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________
的通项公式为________
给出下列四个命题:
① 因为 ,所以
,所以 ;
;
② 由 两边同除
两边同除 ,可得
,可得 ;
;
③ 数列1,4,7,10,…, 的一个通项公式是
的一个通项公式是 ;
;
④ 演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理.
其中正确命题的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
对于正项数列 ,定义
,定义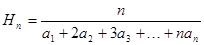 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________
的通项公式为________
已知数列{an}的通项公式为an= (-1)n n,则a4=_____.
已知数列 ,且通项公式分别为
,且通项公式分别为 ,现抽出数列
,现抽出数列 中所有相同的项并按从小到大的顺序排列成一个新的数列
中所有相同的项并按从小到大的顺序排列成一个新的数列 ,则可以推断
,则可以推断 (用
(用 表示(
表示( )).
)).
对数列 ,若区间
,若区间 满足下列条件:
满足下列条件:
①
 ;②
;②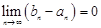 ,
,
则称 为区间套。下列选项中,可以构成区间套的数列是( )
为区间套。下列选项中,可以构成区间套的数列是( )
A. ; ; |
B. |
C.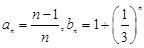 |
D. |