高中数学一阶、二阶线性常系数递归数列的通项公式试题

观察如图三角形数阵，则
（1）若记第n行的第m个数为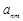，则     ．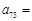
（2）第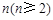行的第2个数是     ．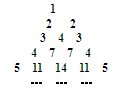

在数列{a_n}中,a₁=1,a_na_n-1=a_n-1+(-1)ⁿ(n≥2,n∈N^*),则的值是(　　)

A．

B．

C．

D．

对于各项均为整数的数列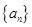，如果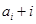(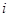=1，2，3，…)为完全平方数，则称数列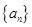具有“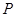性质”．不论数列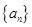是否具有“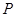性质”，如果存在与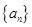不是同一数列的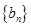，且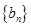同时满足下面两个条件：①是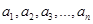的一个排列；②数列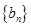具有“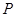性质”，则称数列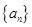具有“变换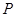性质”．下面三个数列：①数列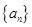的前项和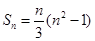；②数列1，2，3，4，5；③1，2，3，…，11.具有“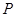性质”的为         ；具有“变换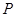性质”的为         .

在数列{}中，已知
（1）求并由此猜想数列{}的通项公式的表达式；
（2）用数学归纳法证明你的猜想。

设，圆的面积为，则      ．

如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2,3出现在第2行；数字6,5,4(从左至右)出现在第3行；数字7,8,9,10出现在第4行，依次类推，则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2，第3行第1个数字为4，…)是__________；(2)第63行从左至右的第4个数字应是__________．

已知数列满足，定义：使乘积为正整数的叫做“期盼数”，则在区间内所有的“期盼数”的和为

A．

B．

C．

D．

已知数列的首项，且，则为 （    ）

A．7

B．15

C．30

D．31

在1到10⁴之间所有形如2ⁿ和3ⁿ(n∈N^*)的数,它们各自之和的差的绝对值为(lg2≈0.3010)(　　)

A．1631

B．6542

C．15340

D．17424

已知数列{a_n}满足:a₁=m(m为正整数),a_n+1=若a₆=1,则m所有可能的值为　　　.

在数列中，已知等于的个位数，则的值是

A．2

B．4

C．6

D．8

数列满足，其前项积为，则=（   ）

A．

B．

C．

D．

数列{a_n}满足a_n+a_n+1=(n∈N^*),a₂=2,S_n是数列{a_n}的前n项和,则S₂₀₁₅为(　　)

A．502

B．504

C．

D．2015

数列-,,-,,…的一个通项公式可以是　　　.

对于任意正整数，定义，对于任意不小于2的正整数，设，
    ，    ．