若数列 满足
满足 =
= (n∈N*,
(n∈N*, 为常数),则称数列
为常数),则称数列 为“调和数列”.已知正项数列
为“调和数列”.已知正项数列 为“调和数列”,且
为“调和数列”,且 ,则
,则 的最大值是 ( )
的最大值是 ( )
| A.10 | B.100 | C.200 | D.400 |
已知数列{an}:a1,a2,a3,…,an,如果数列{bn}:b1,b2,b3,…,bn满足b1=an,bk=ak-1+ak-bk-1,其中k=2,3,…,n,则称{bn}为{an}的“衍生数列”.若数列{an}:a1,a2,a3,a4的“衍生数列”是5,-2,7,2,则{an}为________;若n为偶数,且{an}的“衍生数列”是{bn},则{bn}的“衍生数列”是________.
给定有限单调递增数列 ,数列
,数列 至少有两项)且
至少有两项)且
 ,定义集合
,定义集合 .若对任意点
.若对任意点 ,
,
存在点 使得
使得
 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(1)给出下列四个命题,其中正确的是 .(填上所有正确命题的序号)
①数列 -2,2具有性质
-2,2具有性质 ;
;
②数列 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质 ;
;
③若数列 具有性质
具有性质 ,则
,则 中一定存在两项
中一定存在两项 ,使得
,使得 ;
;
④若数列 具有性质
具有性质 ,
, 且
且 ,则
,则 .
.
(2)若数列 只有2014项且具有性质
只有2014项且具有性质 ,则
,则 的所有项和
的所有项和 .
.
对于正项数列 ,定义
,定义 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________
的通项公式为________
(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列 的“生成数列”是
的“生成数列”是 ,求
,求 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是 ,…,依次将数列
,…,依次将数列 ,
, ,
, ,…的第
,…的第 项取出,构成数列
项取出,构成数列 .
.
探究:数列 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
设 为数列
为数列 的前n项和,若
的前n项和,若
 是非零常数,则称该数列为“和等比数列”.若数列
是非零常数,则称该数列为“和等比数列”.若数列 是首项为
是首项为 ,公差为
,公差为 (
( )的等差数列,且数列
)的等差数列,且数列 是“和等比数列”,则
是“和等比数列”,则 与
与 的关系式为 .
的关系式为 .
对于数对序列,记
,
,其中
表示
和
两个数中最大的数.
(1)对于数对序列,求
的值;
(2)记为
四个数中最小的数,对于由两个数对
组成的数对序列
和
,试分别对
和
两种情况比较
和
的大小;(3)在由五个数对
组成的所有数对序列中,写出一个数对序列
使
最小,并写出
的值.(只需写出结论).
对数列 ,若区间
,若区间 满足下列条件:
满足下列条件:
①
 ;②
;②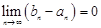 ,
,
则称 为区间套。下列选项中,可以构成区间套的数列是( )
为区间套。下列选项中,可以构成区间套的数列是( )
A. ; ; |
B. |
C.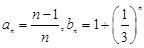 |
D. |
对于正项数列 ,定义
,定义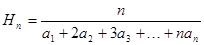 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________
的通项公式为________
已知数列 满足
满足 ,
, (
( ),计算并观察数列
),计算并观察数列 的前若干项,根据前若干项的变化规律推测,
的前若干项,根据前若干项的变化规律推测, .
.