北京市海淀区高三下学期期末练习(二模)理科数学试卷
执行如图所示的程序框图,若输出的 为4,则输入的
为4,则输入的 应为( )
应为( )
| A.2 | B.16 | C.2或8 | D.2或16 |
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
已知 是不等式组
是不等式组 表示的平面区域内的一点,
表示的平面区域内的一点, ,
, 为坐标原点,则
为坐标原点,则 的最大值( )
的最大值( )
| A.2 | B.3 | C.5 | D.6 |
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
一观览车的主架示意图如图所示,其中 为轮轴的中心,距地面32m(即
为轮轴的中心,距地面32m(即 长),巨轮的半径为30m,
长),巨轮的半径为30m,
 m,巨轮逆时针旋转且每12分钟转动一圈.若点
m,巨轮逆时针旋转且每12分钟转动一圈.若点 为吊舱
为吊舱 的初始位置,经过
的初始位置,经过 分钟,该吊舱
分钟,该吊舱 距离地面的高度为
距离地面的高度为 m,则
m,则 =( )
=( )
A. |
B.  |
C. |
D. |
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
已知点 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别是线段
分别是线段 与
与 上的点,则满足与平面
上的点,则满足与平面 平行的直线
平行的直线 有( )
有( )
| A.0条 | B.1条 | C.2条 | D.无数条 |
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
已知集合 ,
, 是集合
是集合 的非空子集,把集合
的非空子集,把集合 中的各元素之和记作
中的各元素之和记作 .
.
①满足 的集合
的集合 的个数为_____;②
的个数为_____;② 的所有不同取值的个数为_____.{本题第一空3分,第二空2分}
的所有不同取值的个数为_____.{本题第一空3分,第二空2分}
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
如图,在三棱柱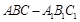 中,
中, 底面
底面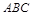 ,
,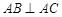 ,
, ,
,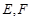 分别是棱
分别是棱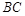 ,
,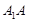 的中点,
的中点, 为棱
为棱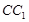 上的一点,且
上的一点,且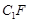 //平面
//平面 .
.
(1)求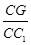 的值;
的值;
(2)求证: ;
;
(3)求二面角 的余弦值.
的余弦值.
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
某单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5.该地区汽车限行规定如下:
| 车尾号 |
0和5 |
1和6 |
2和7 |
3和8 |
4和9 |
| 限行日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
已知椭圆 的离心率为
的离心率为 ,其短轴两端点为
,其短轴两端点为 .
.
(1)求椭圆 的方程;
的方程;
(2)若 是椭圆
是椭圆 上关于
上关于 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与 轴分别交于点
轴分别交于点 .判断以
.判断以 为直径的圆是否过点
为直径的圆是否过点 ,并说明理由.
,并说明理由.
来源:2014届北京市海淀区高三下学期期末练习(二模)理科数学试卷
 的值为( )
的值为( )



 “
“ ,有
,有 成立”,则
成立”,则 为( )
为( ) ,有
,有 成立
成立 ,有
,有 成立
成立 的圆心到极轴的距离为( )
的圆心到极轴的距离为( )



 单调递增且满足
单调递增且满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 的
的 的取值范围是________.
的取值范围是________. 的一条渐近线为
的一条渐近线为 ,则双曲线的离心率为________.
,则双曲线的离心率为________. 的展开式中
的展开式中 的系数是10,则实数
的系数是10,则实数 的值是
的值是 
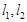 是曲线
是曲线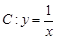 的两条互相平行的切线,则
的两条互相平行的切线,则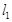 与
与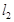 的距离的最大值为_____.
的距离的最大值为_____.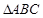 中,
中,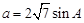 且
且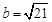 .
.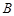 的大小;
的大小;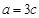 ,求
,求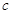 的值.
的值.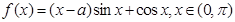 .
.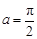 时,求函数
时,求函数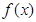 值域;
值域;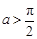 时,求函数
时,求函数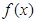 的单调区间.
的单调区间. ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 ,…,实施
,…,实施 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
, .
. ,求
,求 和
和 的值;
的值; 的极差为
的极差为 且
且 ,若
,若 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号