江苏省徐州市五县二区高一期中考试数学试卷
设等差数列 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 ,则下列结论中正确的有 .(填序号)
,则下列结论中正确的有 .(填序号)
①此数列的公差 ;
;
② ;
;
③ 是数列
是数列 的最大项;
的最大项;
④ 是数列
是数列 中的最小项.
中的最小项.
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
某货轮在航行中不幸遇险,发出呼救信号,我海军护卫舰在A处获悉后,测得该货轮在北偏东45º方向距离为10海里的C处,并测得货轮正沿北偏东105º的方向、以每小时9海里的速度向附近的小岛靠拢。我海军护卫舰立即以每小时21海里的速度前去营救;则护卫舰靠近货轮所需的时间是 小时
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
已知各项均为正数的等比数列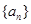 中,
中,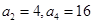 .
.
(1)求公比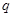 ;
;
(2)若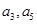 分别为等差数列
分别为等差数列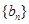 的第3项和第5项,求数列
的第3项和第5项,求数列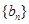 的通项公式.
的通项公式.
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
已知函数 ,
, ,
, .
.
(1)求函数 的值域;
的值域;
(2)若函数 的最小正周期为
的最小正周期为 ,则当
,则当 时,求
时,求 的单调递减区间.
的单调递减区间.
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
在斜三角形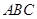 中,角A,B,C的对边分别为 a,b,c.
中,角A,B,C的对边分别为 a,b,c.
(1)若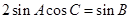 ,求
,求 的值;
的值;
(2)若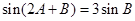 ,求
,求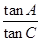 的值.
的值.
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.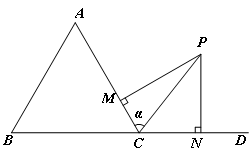
来源:2013-2014学年江苏省徐州市五县二区高一期中考试数学试卷
 中,
中, ,则
,则 =____ __
=____ __ 中,
中,  ,那么此数列的前10项和
,那么此数列的前10项和 = .
= . 的三内角
的三内角 成等差数列,且
成等差数列,且 ,则
,则 = .
= . ,则a=_________.
,则a=_________. ,
, ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4, ,
, ,
, ,-1五个实数成等
,-1五个实数成等 = .
= . 为锐角,
为锐角, 则
则 .
. 的前n项和为
的前n项和为 ,则
,则 = .
= . 的前
的前 项和
项和 ,则
,则 .
. 的括号中,填写一个锐角,使得等式成立,这个锐角是 .
的括号中,填写一个锐角,使得等式成立,这个锐角是 . ,则该三角形的面积的最大值为 .
,则该三角形的面积的最大值为 . 内角
内角 所对的边分别是
所对的边分别是 ,且
,且 .
. ,求
,求 的值;
的值; 的值域.
的值域. 粤公网安备 44130202000953号
粤公网安备 44130202000953号