江西省鹰潭市高三第二次模拟考试理科数学试卷
某车间共有6名工人,他们某日加工零件个数的茎叶图如上图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为( ) 
A.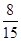 |
B.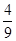 |
C.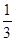 |
D.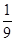 |
下列四个命题:
①利用计算机产生0~1之间的均匀随机数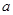 ,则事件“
,则事件“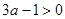 ”发生的概率为
”发生的概率为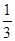 ;
;
②“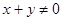 ”是“
”是“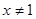 或
或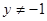 ”的充分不必要条件;
”的充分不必要条件;
③命题“在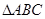 中,若
中,若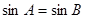 ,则
,则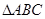 为等腰三角形”的否命题为真命题;
为等腰三角形”的否命题为真命题;
④如果平面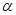 不垂直于平面
不垂直于平面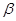 ,那么平面
,那么平面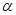 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面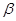 。
。
其中说法正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
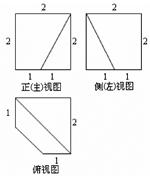
正方形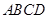 的边长为2,点
的边长为2,点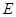 、
、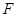 分别在边
分别在边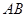 、
、 上,且
上,且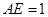 ,
,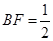 ,将此正
,将此正
方形沿 、
、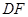 折起,使点
折起,使点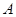 、
、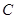 重合于点
重合于点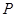 ,则三棱锥
,则三棱锥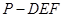 的体积是( )
的体积是( )
A.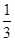 |
B.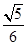 |
C.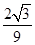 |
D.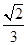 |
设函数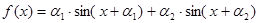 ,其中
,其中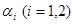 为已知实常数,
为已知实常数,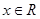 ,则下列命题中错误的是( )
,则下列命题中错误的是( )
A.若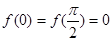 ,则 ,则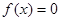 对任意实数 对任意实数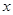 恒成立; 恒成立; |
B.若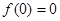 ,则函数 ,则函数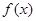 为奇函数; 为奇函数; |
C.若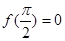 ,则函数 ,则函数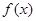 为偶函数; 为偶函数; |
D.当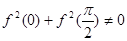 时,若 时,若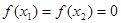 ,则 ,则 . . |
已知函数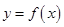 定义域为
定义域为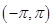 ,且函数
,且函数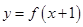 的图象关于直线
的图象关于直线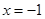 对称,当
对称,当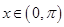 时,
时,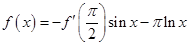 ,(其中
,(其中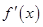 是
是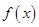 的导函数),若
的导函数),若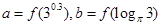 ,
,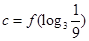 ,则
,则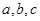 的大小关系是( )
的大小关系是( )
A. |
B. |
C. |
D. |
设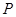 是不等式组
是不等式组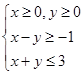 表示的平面区域内的任意一点,向量
表示的平面区域内的任意一点,向量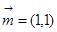 ,
,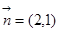 ,若
,若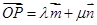 (
(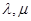 为实数),则
为实数),则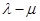 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.-1 | D.-2 |
对于各项均为整数的数列 ,如果
,如果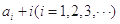 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:①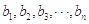 是
是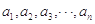 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列:
①数列1,2,3,4,5; ②数列1,2,3, ,11,12; ③数列 的前n项和为
的前n项和为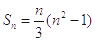 .
.
其中具有“P性质”或“变换P性质”的有( )
| A.③ | B.①③ | C.①② | D.①②③ |
已知直线: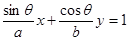 (
(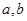 为给定的正常数,
为给定的正常数,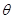 为参数,
为参数,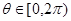 )构成的集合为S,给出下列命题:
)构成的集合为S,给出下列命题:
①当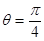 时,
时,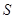 中直线的斜率为
中直线的斜率为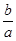 ;
;
②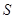 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当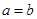 时,存在某个定点,该定点到
时,存在某个定点,该定点到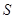 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当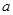 >
>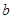 时,
时,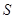 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为 ;
;
其中正确的是 (写出所有正确命题的编号).
为喜迎马年新春佳节,某商场在正月初六进行抽奖促销活动,当日在该店消费满500元的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有 “马”“上”“有”“钱”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“钱”字球,则停止取球.获奖规则如下:依次取到标有“马”“上”“有”“钱”字的球为一等奖;不分顺序取到标有“马”“上”“有”“钱”字的球,为二等奖;取到的4个球中有标有“马”“上”“有”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
如图,在直三棱柱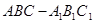 中,
中,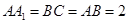 ,
,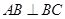 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。
(1)求二面角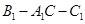 的大小。
的大小。
(2)证明:在AB上存在一个点Q,使得平面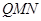 ⊥平面
⊥平面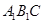 ,
,
并求出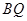 的长度。
的长度。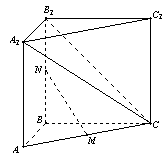
如图: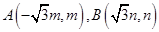 两点分别在射线
两点分别在射线 上移动,
上移动,
且 ,
,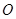 为坐标原点,动点
为坐标原点,动点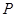 满足
满足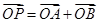
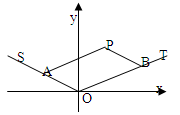
(1)求点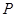 的轨迹
的轨迹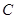 的方程;
的方程;
(2)设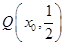 ,过
,过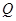 作(1)中曲线
作(1)中曲线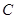 的两条切线,切点分别
的两条切线,切点分别
为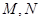 ,①求证:直线
,①求证:直线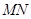 过定点;
过定点;
②若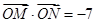 ,求
,求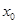 的值。
的值。
 ,若
,若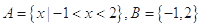 ,
,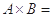 ( )
( )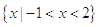
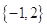
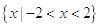
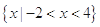
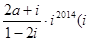 是虚数单位)为纯虚数,则实数
是虚数单位)为纯虚数,则实数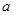 的值为( )
的值为( )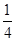
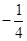
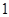
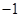
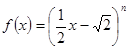 ,其中
,其中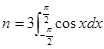 ,则
,则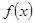 的展开式中
的展开式中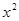 的系数为( )
的系数为( )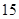
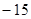
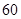
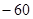
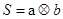 ,运算原理如下图所示,则式子
,运算原理如下图所示,则式子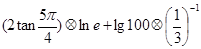 的值为 。
的值为 。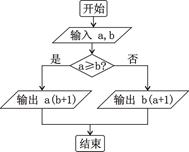

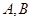 两点,若
两点,若 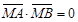 则
则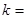
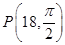 引圆
引圆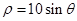 的两条切线
的两条切线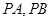 ,切点分别为
,切点分别为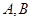 ,则线段
,则线段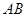 的长为 .
的长为 .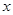 的不等式
的不等式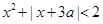 至少有一个正数解,则实数
至少有一个正数解,则实数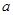 的取值范围是 。
的取值范围是 。 中,三个内角A,B,C所对的边分别是a,b,c,且
中,三个内角A,B,C所对的边分别是a,b,c,且 .
. 的大小;
的大小; 的取值范围.
的取值范围.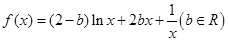 .
.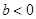 时,求
时,求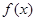 的单调区间;
的单调区间;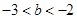 时,若存在
时,若存在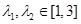 , 使得
, 使得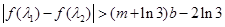 成立,求实数
成立,求实数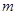 的取值范围.
的取值范围.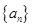 满足:
满足: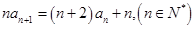 且
且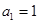 .
.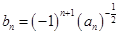 ,数列
,数列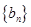 的前项和为
的前项和为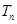 ,求证:
,求证: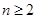 时,
时, 且
且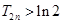
 粤公网安备 44130202000953号
粤公网安备 44130202000953号