某种汽车购买时费用为 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年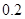 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增.
(1)设使用 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
相关知识点
推荐套卷
某种汽车购买时费用为 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年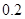 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增.
(1)设使用 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).