高中数学一阶、二阶线性常系数递归数列的通项公式试题

已知（）是曲线上的点，，是数列的前项和，且满足，， ．
（1）证明：数列（）是常数数列；
（2）确定的取值集合，使时，数列是单调递增数列；
（3）证明：当时，弦（）的斜率随单调递增

在轴的正方向上，从左向右依次取点列 ，以及在第一象限内的抛物线上从左向右依次取点列，使（）都是等边三角形，其中是坐标原点，则第2005个等边三角形的边长是      ．

甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为a_n%,B喷雾器中药水的浓度为b_n%.
(1)证明a_n+b_n是一个常数.
(2)求a_n与a_n-1的关系式.
(3)求a_n的表达式.

已知数列满足，给出下列命题：
①当时，数列为递减数列
②当时，数列不一定有最大项
③当时，数列为递减数列
④当为正整数时，数列必有两项相等的最大项
请写出正确的命题的序号____

如图，互不相同的点A₁，A₂，…，A_n，…和B₁，B₂，…，B_n，…分别在角O的两条边上，所有A_nB_n相互平行，且所有梯形A_nB_nB_n＋1A_n＋1的面积均相等，设OA_n＝a_n.若a₁＝1，a₂＝2，则数列{a_n}的通项公式是________．

正项数列的前项和满足:
(1)求数列的通项公式;
(2)令,求数列的前项和.

设函数f(x)=+sinx的所有正的极小值点从小到大排成的数列为{x_n}.
(1)求数列{x_n}的通项公式.
(2)设{x_n}的前n项和为S_n,求sinS_n.

已知正项数列满足：，数列的前项和为，且满足，.
（1）求数列和的通项公式；
（2）设，数列的前项和为，求证：.

在一个数列中，如果对任意,都有为常数，那么这个数列叫做等积数列，叫做这个数列的公积．已知数列是等积数列，且，公积为，记的前项和为，则：
（1）          ．
（2）           ．

若数列{a_n}满足＝d(n∈N^*，d为常数)，则称数列{a_n}为“调和数列”．已知正项数列为“调和数列”，且b₁＋b₂＋…＋b₉＝90，则b₄·b₆的最大值是(　　)．

A．10

B．100

C．200

D．400

对于自然数数组，如下定义该数组的极差：三个数的最大值与最小值的差.如果的极差，可实施如下操作：若中最大的数唯一，则把最大数减2，其余两个数各增加1；若中最大的数有两个，则把最大数各减1，第三个数加2，此为一次操作，操作结果记为，其级差为.若，则继续对实施操作，…，实施次操作后的结果记为，其极差记为.例如：，.
（1）若，求和的值；
（2）已知的极差为且，若时，恒有，求的所有可能取值；
（3）若是以4为公比的正整数等比数列中的任意三项，求证：存在满足.

在数列中，
（1）证明是等比数列，并求的通项公式；
（2）求的前n项和

已知数列a_n＝n－16，b_n＝(－1)ⁿ|n－15|，其中n∈N^*.
(1)求满足a_n＋1＝|b_n|的所有正整数n的集合；
(2)若n≠16，求数列的最大值和最小值；
(3)记数列{a_nb_n}的前n项和为S_n，求所有满足S_2m＝S_2n(m＜n)的有序整数对(m，n)．

设不等式组所表示的平面区域为D_n，记D_n内的整点个数为a_n(n∈N^*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{a_n}的通项公式；
(2)记数列{a_n}的前n项和为S_n，且T_n＝.若对于一切的正整数n，总有T_n≤m，求实数m的取值范围．

对于各项均为整数的数列，如果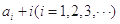为完全平方数，则称数列具有“P性质”，如果数列不具有“P性质”，只要存在与不是同一数列的，且同时满足下面两个条件：①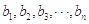是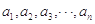的一个排列；②数列具有“P性质”，则称数列具有“变换P性质”，下面三个数列：
①数列1，2，3，4，5； ②数列1，2，3， ，11,12； ③数列的前n项和为.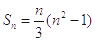
其中具有“P性质”或“变换P性质”的有(     )

A．③

B．①③

C．①②

D．①②③