有限数列D: ,
, ,…,
,…, ,其中
,其中 为数列D的前
为数列D的前 项和,定义
项和,定义 为D的“德光和”,若有
为D的“德光和”,若有 项的数列
项的数列 ,
, ,…,
,…, 的“德光和”为
的“德光和”为 ,则有
,则有 项的数列8,
项的数列8, ,
, ,…,
,…, 的“德光和”为
的“德光和”为
设 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
 .
.
(1)求满足“对任意的 ,
, ,都有
,都有 ”的有序数组(
”的有序数组( )的个数
)的个数 ;
;
(2)若对任意的 ,
, ,
, ,都有
,都有 成立,求满足“存在
成立,求满足“存在 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数
对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项与偶数项各有什么特点?并加以说明.
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项与偶数项各有什么特点?并加以说明.
如果数列 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意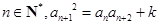 都成立,则称这样的数列
都成立,则称这样的数列 为“类等比数列” .由此等比数列必定是“类等比数列” .问:
为“类等比数列” .由此等比数列必定是“类等比数列” .问:
(1)各项均不为0的等差数列 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.
(2)若数列 为“类等比数列”,且
为“类等比数列”,且 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例.
(3)若数列 为“类等比数列”,且
为“类等比数列”,且 ,
, (a,b为常数),求数列
(a,b为常数),求数列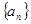 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
.
若数列 满足
满足 且
且 (其中
(其中 为常数),
为常数), 是数列
是数列 的前
的前 项和,数列
项和,数列 满足
满足 .
.
(1)求 的值;
的值;
(2)试判断 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求 (用
(用 表示).
表示).
数列 的前n项和为
的前n项和为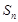 ,
, ,且对任意的
,且对任意的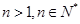 均满足
均满足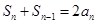 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
,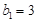 ,
,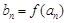 (
( ),求数列
),求数列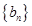 的前
的前 项和
项和 .
.
某市为控制大气PM2.5的浓度,环境部门规定:该市每年的大气主要污染物排放总量不能超过55万吨,否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨,通过技术改造和倡导绿色低碳生活等措施,此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时,因为经济发展和人口增加等因素,每年又新增加大气主要污染物排放量 万吨.
万吨.
(1)从2014年起,该市每年大气主要污染物排放总量(万吨)依次构成数列 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;
(2)证明:数列 是等比数列;
是等比数列;
(3)若该市始终不需要采取紧急限排措施,求m的取值范围.
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为 。求
。求
(1) 及
及 与
与
 的关系式;
的关系式;
(2)数列 的通项公式
的通项公式 ,并证明:
,并证明:

某种汽车购买时费用为 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增.
(1)设使用 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
已知 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
.
(1)证明:数列 (
( )是常数数列;
)是常数数列;
(2)确定 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 是单调递增数列;
是单调递增数列;
(3)证明:当 时,弦
时,弦 (
( )的斜率随
)的斜率随 单调递增
单调递增
对于自然数数组 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 的极差
的极差 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 实施操作
实施操作 ,…,实施
,…,实施 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
, .
.
(1)若 ,求
,求 和
和 的值;
的值;
(2)已知 的极差为
的极差为 且
且 ,若
,若 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值;
(3)若 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在 满足
满足 .
.
已知数列 满足
满足
(1)分别求 的值。
的值。
(2)猜想 的通项公式
的通项公式 ,并用数学归纳法证明。
,并用数学归纳法证明。