上海市闵行区高三三模冲刺理科数学试卷
某班级有4名学生被复旦大学自主招生录取后,大学提供了3个专业由这4名学生选择,每名学生只能选择一个专业,假设每名学生选择每个专业都是等可能的,则这3个专业都有学生选择的概率是 .
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
设 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在点P,满足
的左、右焦点,若在双曲线右支上存在点P,满足 且
且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
下图揭示了一个由区间 到实数集
到实数集 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段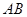 (不包括端点)上的点
(不包括端点)上的点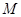 一一对应(图一),将线段
一一对应(图一),将线段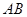 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线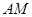 与
与 轴交于点
轴交于点 ,由此得到一个函数
,由此得到一个函数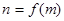 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( ) ;
;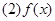 是偶函数;
是偶函数;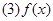 在其定义域上是增函数;
在其定义域上是增函数; 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4) | B.(1)(2)(3) |
| C.(1)(2)(4) | D.(1)(2)(3)(4). |
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
已知复数 (
( 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为 ,点
,点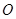 是坐标原点.
是坐标原点.
(1)若 ,求
,求 的值;
的值;
(2)若 点的横坐标为
点的横坐标为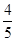 ,求
,求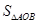 .
.
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形, (
( 为圆柱的高,
为圆柱的高,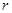 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
(1)写出 关于
关于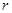 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该储油罐的建造费用最小时的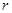 的值.
的值.
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
已知椭圆C过点 ,两焦点为
,两焦点为 、
、 ,
, 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线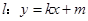 与该椭圆交于两个不同点
与该椭圆交于两个不同点 、
、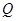 ,且直线
,且直线 、
、 、
、 的斜率依次成等比数列.
的斜率依次成等比数列.
(1)求椭圆C的方程;
(2)求直线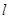 的斜率
的斜率 ;
;
(3)求 面积的范围.
面积的范围.
来源:2014届上海市闵行区高三三模冲刺理科数学试卷
 ,
, ,则
,则 等于 .
等于 . 的定义域是 .
的定义域是 . ,则
,则 .
. 的实部与虚部相等,则
的实部与虚部相等,则 的值为 .
的值为 . ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的最小值为 .
的最小值为 .  的前n项和为
的前n项和为 ,已知
,已知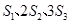 成等差数列,则数列
成等差数列,则数列 ,若
,若 ,则
,则 .
. 的正方形的四棱锥
的正方形的四棱锥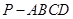 中,已知
中,已知 ,且
,且 ,则直线
,则直线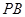 与平面
与平面 所成的角大小为 .
所成的角大小为 . 
 与直线
与直线 的两个交点之间的距离为 .
的两个交点之间的距离为 .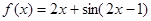 图像的对称中心是 .
图像的对称中心是 . 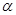 的终边在第一象限,函数
的终边在第一象限,函数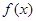 的定义域为
的定义域为 ,且
,且 ,当
,当 时,有
时,有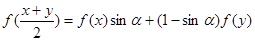 ,则使等式
,则使等式 成立的
成立的 个非零向量
个非零向量 ,且
,且 ,各向量的横坐标和纵坐标均为非负实数,若
,各向量的横坐标和纵坐标均为非负实数,若 (常数),则
(常数),则 的最小值为 .
的最小值为 . 的值域相同的函数为( )
的值域相同的函数为( )
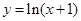


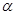 终边上有一点
终边上有一点 ,则下列各点中在角
,则下列各点中在角 的终边上的点是 ( )
的终边上的点是 ( )

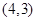
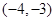
 各项的和为
各项的和为 ,第二项为
,第二项为 ,则该数列的公比为 ( )
,则该数列的公比为 ( )
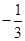
 .
.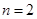 ,
,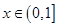 时,若不等式
时,若不等式 恒成立,求
恒成立,求 的范围;
的范围; 在
在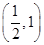 内零点的个数,并说明理由.
内零点的个数,并说明理由. 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意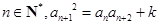 都成立,则称这样的数列
都成立,则称这样的数列 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由. (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例. (a,b为常数),求数列
(a,b为常数),求数列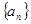 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号