已知正项数列 满足:
满足: ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知正项数列 满足:
满足: ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为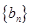 ,并称
,并称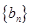 为数列
为数列 的
的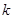 项子列.例如数列
项子列.例如数列 、
、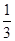 、
、 、
、 为
为 的一个
的一个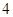 项子列.
项子列.
(1)试写出数列 的一个
的一个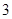 项子列,并使其为等比数列;
项子列,并使其为等比数列;
(2)如果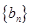 为数列
为数列 的一个
的一个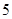 项子列,且
项子列,且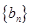 为等差数列,证明:
为等差数列,证明: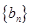 的公差
的公差 满足
满足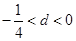 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明: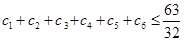 .
.
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列
,数列 的首项
的首项 ,
, .
.
(1)求函数 的表达式;(2)求数列
的表达式;(2)求数列 的前
的前 项和
项和 .
.
对于项数为 的有穷数列数集
的有穷数列数集 ,记
,记
 ,即
,即 为
为 、
、 、
、 、
、 中的最大值,并称数列
中的最大值,并称数列 是
是 的控制数列.如
的控制数列.如 、
、 、
、 、
、 、
、 的控制数列是
的控制数列是 、
、 、
、 、
、 、
、 .
.
(1)若各项均为正整数的数列 的控制数列为
的控制数列为 、
、 、
、 、
、 、
、 ,写出所有的
,写出所有的 ;
;
(2)设 是
是 的控制数列,满足
的控制数列,满足 (
( 为常数,
为常数, 、
、 、
、 、
、 ).求证:
).求证:
 .
.
数列{an}的前n项和记为Sn,已知a1=1,an+1= Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:
(1)数列 是等比数列;
是等比数列;
(2)Sn+1=4an.
设不等式组 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,且Tn= .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
正项数列{an}的前项和满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn= ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn< .
.
设数列{an}的前n项和为Sn.已知a1=1, =an+1-
=an+1- n2-n-
n2-n- ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
.
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
已知an=
(1)求数列{an}的前10项和S10;
(2)求数列{an}的前2k项和S2k.
已知数列 的通项公式an=
的通项公式an= (n∈N*),求数列前30项中的最大项和最小项.
(n∈N*),求数列前30项中的最大项和最小项.
已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.