江西省上饶市高三第二次模拟考试文科数学试卷
在数列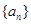 中,
中,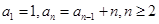 .为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是 ( )
.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是 ( )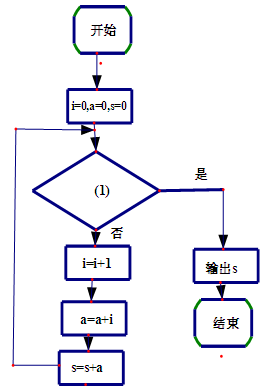
A. |
B. |
C.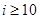 |
D.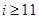 |
设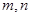 是两条不同的直线,
是两条不同的直线, 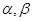 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若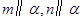 ,则 ,则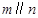 |
B.若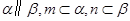 ,则 ,则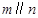 |
C.若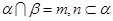 ,则 ,则 |
D.若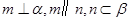 ,则 ,则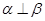 |
以下命题中:①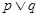 为假命题,则
为假命题,则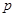 与
与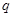 均为假命题
均为假命题
②对具有线性相关的变量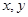 有一组观测数据
有一组观测数据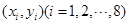 ,其回归直线方程是
,其回归直线方程是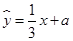 ,且
,且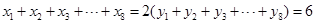 ,则实数
,则实数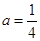
③对于分类变量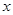 与
与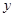 它们的随机变量
它们的随机变量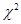 的观测值
的观测值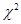 来说
来说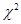 越小.“
越小.“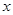 与
与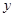 有关联”的把握程度越大
有关联”的把握程度越大
④已知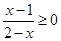 ,则函数
,则函数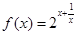 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
已知函数 在一个周期内的图像如图所示,其中P,Q分别是这段图像的最高点和最低点,M,N是图像与x轴的交点,且
在一个周期内的图像如图所示,其中P,Q分别是这段图像的最高点和最低点,M,N是图像与x轴的交点,且 ,则A的值为( )
,则A的值为( )
A. |
B. |
C. |
D. |
过抛物线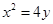 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且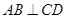 ,则
,则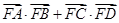 的最大等于 ( )
的最大等于 ( )
A.-4
B.-16
C.4
D.-8
如图,不规则四边形ABCD中,AB和CD是线段,AD和BC是圆弧,直线 于E,当
于E,当 从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设
从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设 ,左侧部分面积为
,左侧部分面积为 ,则
,则 关于
关于 的图像大致为( )
的图像大致为( )

某校从参加高三年级期末考试的学生中随机抽取60名学生,将其数学成绩分成六段:[40,50),[50,60), …[90,100),它的频率分布直方图如图所示,则该批学生中成绩不低于60分的人数为___________.
过双曲线 上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若
上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若 ,则该双曲线的离心率为____.
,则该双曲线的离心率为____.
如图所示将若干个点摆成三角形,每条边(包括两个端点)有 个点,相应的图案中总的点数记为
个点,相应的图案中总的点数记为 ,则
,则 _______.
_______.
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为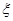 ,求概率P
,求概率P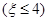 .
.
(2)在正方形ABCD内部随机取一点P,求满足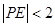 的概率.
的概率.
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A,B的一点,D为AC的中点. 
(1)求该圆锥的侧面积S;
(2)求证:平面PAC 平面POD;
平面POD;
(3)若 ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离.
已知椭圆 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
(1)求椭圆的方程;
(2)求 的面积的最大值.
的面积的最大值.
 对应的点位于 )
对应的点位于 ) 的各项都是正数,且
的各项都是正数,且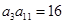 则
则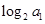 = ( )
= ( ) 若
若 ,则实数
,则实数 ( )
( )
 ,满足
,满足 ,若
,若 且
且 ,则有( )
,则有( )


 上的点向圆
上的点向圆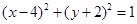 引切线,则切线长的最小值为___________.
引切线,则切线长的最小值为___________.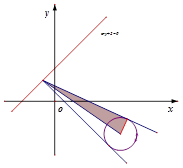
 ,则集合
,则集合 ________
________
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 是
是 三边长,且
三边长,且 ,
, .求角
.求角 及
及 的值.
的值. 满足
满足 .
. 的表达式;
的表达式; ,求
,求 .
.
 时,求
时,求 的极值;
的极值; 时,讨论
时,讨论 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号