湖南省长沙市高考二模文科数学试卷
一平面截一球得到直径为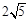 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是( )
cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是( )
| A.12 cm3 | B.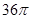 cm3 cm3 |
C. cm3 cm3 |
D.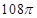 cm3 cm3 |
来源:2014届湖南省长沙市高考二模文科数学试卷
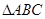 中,角
中,角 的对边分别为
的对边分别为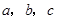 ,则“
,则“ ”是“
”是“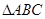 是等腰三角形”的( )
是等腰三角形”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届湖南省长沙市高考二模文科数学试卷
设双曲线 ,离心率
,离心率 ,右焦点
,右焦点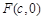 .方程
.方程 的两个实数根分别为
的两个实数根分别为 ,则点
,则点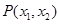 与圆
与圆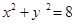 的位置关系( )
的位置关系( )
| A.在圆外 | B.在圆上 | C.在圆内 | D.不确定 |
来源:2014届湖南省长沙市高考二模文科数学试卷
巳知函数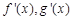 分别是二次函数
分别是二次函数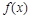 和三次函数
和三次函数 的导函数,它们在同一坐标系内的图象如图所示.
的导函数,它们在同一坐标系内的图象如图所示.
(1)若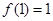 ,则
,则 ;
;
(2)设函数 ,则
,则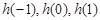 的大小关系为 (用“<”连接).
的大小关系为 (用“<”连接).
来源:2014届湖南省长沙市高考二模文科数学试卷
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| |
支持A方案 |
支持B方案 |
支持C方案 |
| 35岁以下 |
200 |
400 |
800 |
| 35岁以上(含35岁) |
100 |
100 |
400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
来源:2014届湖南省长沙市高考二模文科数学试卷
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB= 60°,FC⊥平面ABCD,AE⊥BD,CB=" CD=" CF.
(1)求证:BD⊥平面AED;
(2)求二面角F—BD—C的正切值.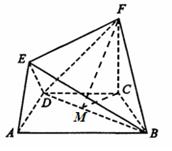
来源:2014届湖南省长沙市高考二模文科数学试卷
已知抛物线 上有一点
上有一点 到焦点
到焦点 的距离为
的距离为 .
.
(1)求 及
及 的值.
的值.
(2)如图,设直线 与抛物线交于两点
与抛物线交于两点 ,且
,且 ,过弦
,过弦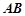 的中点
的中点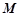 作垂直于
作垂直于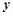 轴的直线与抛物线交于点
轴的直线与抛物线交于点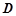 ,连接
,连接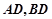 .试判断
.试判断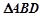 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由. 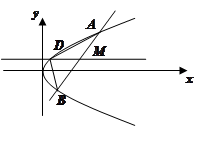
来源:2014届湖南省长沙市高考二模文科数学试卷
 ,则
,则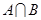 等于( )
等于( )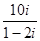 =( )
=( ) ,则下列关系中正确的是( )
,则下列关系中正确的是( ) 中
中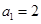 ,公比
,公比 ,记
,记 (即
(即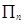 表示数列
表示数列 中值最大的是( )
中值最大的是( )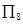
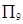
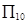


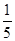
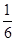

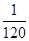
 中,D为AB边上一点,
中,D为AB边上一点,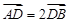 ,
,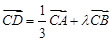 ,则
,则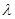 =( )
=( )


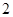
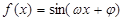
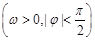 ,满足
,满足 ,
,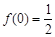 ,则
,则 在区间
在区间 上的最大值与最小值之和为( )
上的最大值与最小值之和为( )
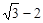
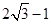

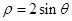 的圆与参数方程
的圆与参数方程 的直线的位置关系是 .
的直线的位置关系是 .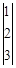
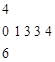 ,则这组数据的平均数等于 .
,则这组数据的平均数等于 . ,则
,则 的最大值为 .
的最大值为 .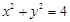 ,在圆M上随机取两点A、B,使
,在圆M上随机取两点A、B,使 的概率为 .
的概率为 .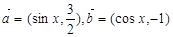
 时,求
时,求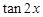 的值;
的值; 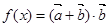 在
在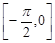 上的值域.
上的值域. 的前n项和为
的前n项和为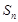 ,
, ,且对任意的
,且对任意的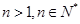 均满足
均满足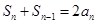 .
. ,
,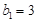 ,
,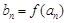 (
( ),求数列
),求数列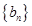 的前
的前 项和
项和 .
. .
.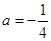 时,求函数
时,求函数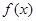 的单调区间;
的单调区间; 时,函数
时,函数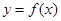 图象上的点都在
图象上的点都在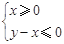 所表示的平面区域内,不等式
所表示的平面区域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  粤公网安备 44130202000953号
粤公网安备 44130202000953号