高中数学随机思想的发展解答题

在一个盒子中，放有标号分别为，，的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为、，记．
（Ⅰ）求随机变量的最大值，并求事件“取得最大值”的概率；
（Ⅱ）求随机变量的分布列和数学期望．

某同学上楼梯的习惯每步走1阶或2阶，现有一个11阶的楼梯 ，该同学从第1阶到第11阶用7步走完。
(1)求该同学恰好有连着三步都走2阶的概率；
(2)记该同学连走2阶的最多步数为ζ，求随机事件ζ的分布列及其期望。

（Ⅰ）求掷骰子的次数为7的概率；
（Ⅱ）求的分布列及数学期望E。

甲，乙两个同学同时报名参加某重点高校年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格.已知甲，乙两人审核过关的概率分别为，，审核过关后，甲，乙两人文化测试合格的概率分别为，.
(1)求甲，乙两人至少有一人通过审核的概率；
(2) 设表示甲，乙两人中获得自主招生入选资格的人数，求的数学期望.

甲、乙两个射手进行射击训练，甲击中目标的概率为，乙击中目标的概率为，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”.
（1）求一个“单位射击组”为“单位进步组”的概率；（2）现要完成三个“单位射击组”，记出现“单位进步组”的次数为，求的分布列与数学期望.

有一个3×3×3的正方体, 它的六个面上均涂上颜色. 现将这个长方体锯成27个1×1×1的小正方体，从这些小正方体中随机地任取1个.
如每次从中任取一个小正方体，确定涂色的面数后，再放回，连续抽取6次，设恰好取到只有一个面涂有颜色的小正方体的次数为. 求的数学期望. 

如图 A B两点有5条线并联，它们在单位时间内能通过的信息依次为2、3、4、3、2，现从中任取三条线且记在单位时间内通过的信息总量为ζ。

（Ⅰ）写出信息总量ζ的分布布列；
（Ⅱ）求信息总量ζ的数学期望。

（1）   求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。
（2）   求甲运动员射击环数的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？

（Ⅰ）求该人在4次投掷中恰有三次投入红袋的概率;
（Ⅱ）求该人两次投掷后得分的数学期望

（本小题满分12分）某社区举办2010年上海世博会知识宣传活动，进行现场抽奖，抽奖规则是：盒中装有10张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”（世博会吉祥物）图案，参加者每次从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖．
（1）活动开始后，一位参加者问：盒中有几张“海宝”卡？主持人笑说：我只知道若从盒中抽两张都不是“海宝”卡的概率是，求抽奖者获奖的概率；
（2）现有甲乙丙丁四人依次抽奖，抽后放回，另一个人再抽，用表示获奖的人数，求的分布列及．

分别写在六张卡片上，放在一盒子中。 （1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数卡片则停止抽取，否则继续进行，求抽取次数的分布列和数学期望．

（本小题满分14分）将3个完全相同的小球随机地放入编号依次为1，2，3，4，5的盒子里，用随机变量 表示有球盒子编号的最大值．（Ⅰ）求；（Ⅱ）求的分布列和数学期望．

甲、乙、丙3人投篮,投进的概率分别是 .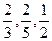
(Ⅰ)现3人各投篮1次,分别求3人都没有投进和3人中恰有2人投进的概率.
(Ⅱ)用ξ表示乙投篮4次的进球数,求随机变量ξ的概率分布及数学期望Eξ.

一盒中装有分别标记着1，2，3，4数字的4个小球，每次从袋中取出一只球，设每只小球被取出的可能性相同.（I）若每次取出的球不放回盒中，现连续取三次球，求恰好第三次取出的球的标号为最大数字的球的概率；（II）若每次取出的球放回盒中，然后再取出一只球，现连续取三次球，这三次取出的球中标号最大数字为，求的概率分布列与期望.

一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：
（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数的分布列和数学期望.