高中数学随机思想的发展解答题

某校积极响应《全面健身条例》，把周五下午5：00~6：00定为职工活动时间，并成立了行政和教师两支篮球队，但由于工作性质所限，每月（假设为4周）每支球队只能组织两次活动，且两支球队的活动时间是相互独立的。
（1）求这两支球队每月两次都在同一时间活动的频率；
（2）设这两支球队每月能同时活动的次数为，求随机变量的分布列和数学期望。

设一台机器在一天内发生故障的概率为0．2，机器发生故障时全天停止工作，一周5个工作日里无故障可获利润10万元，发生一次故障可获利5万元，发生两次故障没有利润，发生三次或三次以上故障就亏损2万元，求一周内平均获利多少？

某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.
（1）已知甲、乙两种产品每一道工序的加工结
果为A级的概率如表一所示，分别求生产
出的甲、乙产品为一等品的概率P_甲、P_乙；
（2）已知一件产品的利润如表二所示，用ξ、
    η分别表示一件甲、乙产品的利润，在
（I）的条件下，求ξ、η的分布列及
Eξ、Eη；
（3）已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名，可用资.

项目 产品 工人（名） 资金（万元） 甲 8 8 乙 2 10

    金60万元.设x、y分别表示生产甲、乙产

用 量

    品的数量，在（II）的条件下，x、y为何

    值时， 最大？最大值是多少？
（解答时须给出图示）

2009年一项关于16艘轮船的研究中，船的吨位区间位于192吨到3246吨，船员的人数从5人到32人，船员的人数关于船的吨位的回归分析得到如下结果：船员人数=9．1+0．006×吨位．
（1）假定两艘轮船吨位相差1000吨，船员平均人数相差多少？
（2）对于最小的船估计的船员数为多少？对于最大的船估计的船员数是多少？

某公司“咨询热线”电话共有8路外线，经长期统计发现，在8点到10点这段时间内，外线电话同时打入情况如下表所示：

电话同时 打入个数	0	1	2	3	4	5	6	7	8
概率	0．13	0．35	0．27	0．14	0．08	0．02	0．01	0	0

（1）若这段时间内，公司只安排了2位接线员（一个接线员一次只能接一个电话）
①求至少一路电话不能一次接通的概率；
②在一周五个工作日中，如果有三个工作日的这段时间（8点至10点）内至少一路电话不能一次接通，那么公司的形象将受到损害，现用至少一路电话不能一次接通的概率表示公司形象的“损害度”，求上述情况下公司形象的“损害度”．
（2）求一周五个工作日的这段时间（8点至10点）内，电话同时打入数X的均值．

张华同学上学途中必须经过四个交通岗，其中在岗遇到红灯的概率均为，在岗遇到红灯的概率均为．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
（1）若，就会迟到，求张华不迟到的概率；（2）求EX．

掷3枚均匀硬币一次，求正面个数与反面个数之差X的分布列，并求其均值和方差．

某种项目的射击比赛，开始时在距目标100m处射击，如果命中记3分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已在150m处，这时命中记2分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已在200m处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分．已知射手甲在100m处击中目标的概率为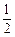，他的命中率与目标的距离的平方成反比，且各次射击都是独立的．
（1）求这位射手在三次射击中命中目标的概率；
（2）求这位射手在这次射击比赛中得分的均值．

有三张形状、大小、质地完全一致的卡片，在每张卡片上分别写上0，1，2，现从中任意抽取一张，将其上的数字记作x，然后放回，再抽取一张，将其上的数字记作y，令．
（1）求X所取各值的概率；
（2）求随机变量X的均值与方差．

甲、乙两名射击运动员，甲射击一次命中环的概率为，乙射击一次命中环的概率为，若他们独立的射击两次，设乙命中环的次数为，则，为甲与乙命中环的次数的差的绝对值．求的值及的分布列及数学期望．

学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有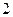人，会跳舞的有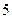人，现从中选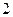人．设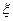为选出的人中既会唱歌又会跳舞的人数，且．
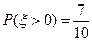（1）求文娱队的人数；
（2）写出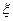的概率分布列并计算．

某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08，选修甲和乙而不选修丙的概率是0.12，至少选修一门课的概率是0.88，用表示该学生选修的课程门数和没有 选修的课程门数的乘积.
（1）记“函数f（x）=x²+·x为R上的偶函数”为事件A，求事件A的概率；
（2）求的概率分布和数学期望.

一个袋中装有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是.若袋中共有10个球,
（1）求白球的个数；
（2）从袋中任意摸出3个球，记得到白球的个数为，求随机变量的数学期望E().

设在12个同类型的零件中有2个次品，抽取3次进行检验，每次抽取一个，并且取出不再放回，若以ξ和分别表示取出次品和正品的个数.
（1）求的概率分布、期望值及方差；
（2）求的概率分布、期望值及方差.

某地区的一个季节下雨天的概率是0.3，气象台预报天气的准确率为0.8.某厂生产的产品当天怕雨，若下雨而不做处理，每天会损失3 000元，若对当天产品作防雨处理，可使产品不受损失，费用是每天500元.
（1）若该厂任其自然不作防雨处理，写出每天损失的概率分布，并求其平均值；
（2）若该厂完全按气象预报作防雨处理，以表示每天的损失，写出的概率分布.
计算的平均值，并说明按气象预报作防雨处理是否是正确的选择？