一个射箭运动员在练习时只记射中 环和
环和 环的成绩,未击中
环的成绩,未击中 环或
环或 环就以
环就以 环记.该远动员在练习时击中
环记.该远动员在练习时击中 环的概率为
环的概率为 ,击中
,击中 环的概率为
环的概率为 ,既未击中
,既未击中 环也未击中
环也未击中 环的概率为
环的概率为 (
( ,
, ,
, ),如果已知该运动员一次射箭击中环数的期望为
),如果已知该运动员一次射箭击中环数的期望为 环,则当
环,则当 取最小值时,
取最小值时, 的值为()
的值为()
A. |
B. |
C. |
D. |
如果袋中有六个红球,四个白球,从中任取一球,确认颜色后放回,重复摸取四次,设X为取得红球的次数,那么X的均值为()
A. |
B. |
C. |
D. |
若离散型随机变量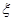 的分布列为:则随机变量
的分布列为:则随机变量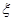 的期望为()
的期望为()
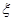 |
0 |
1 |
2 |
3 |
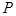 |
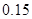 |
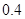 |
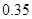 |
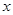 |
A.1.4 B.0.15 C.1.5 D.0.14
一牧场有10头牛,因误食含有病毒的饲料而被感染,已知该病的发病率为 .设发病的牛的头数为
.设发病的牛的头数为 ,则
,则 等于()
等于()
A. |
B. |
C. |
D. |
已知随机变量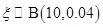 ,随机变量
,随机变量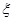 的数学期望
的数学期望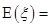 ()
()
A.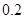 |
B.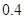 |
C.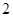 |
D. |
有一批产品,其中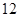 件是正品,
件是正品,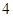 件是次品,有放回的任取
件是次品,有放回的任取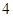 件,若
件,若 表示取到次品的件数,则
表示取到次品的件数,则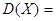
A.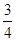 |
B.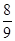 |
C.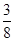 |
D.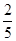 |
设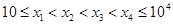 ,
, . 随机变量
. 随机变量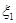 取值
取值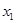 、
、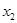 、
、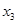 、
、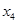 、
、 的概率均为0.2,随机变量
的概率均为0.2,随机变量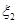 取值
取值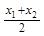 、
、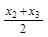 、
、 、
、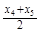 、
、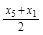 的概率也为0.2.若记
的概率也为0.2.若记 、
、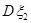 分别为
分别为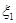 、
、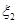 的方差,则 ()
的方差,则 ()
A. > >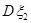 |
B. = =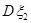 |
C. < <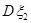 |
D. 与 与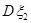 的大小关系与 的大小关系与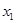 、 、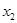 、 、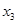 、 、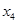 的取值有关 的取值有关 |
、已知随机变量 的分布列是其中
的分布列是其中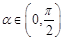 ,则
,则
 |
-1 |
0 |
2 |
| P |
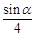 |
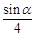 |
 |
A、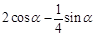 B、
B、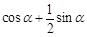 C、0 D、1
C、0 D、1
抛掷两枚骰子,当至少有一枚5点或6点出现时,就说试验成功,则在30次独立重复试验中成功的次数X的数学期望是
A.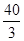 |
B.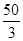 |
C.10 | D.20 |
以每束1.6元价格处理.根据前五年销售情况预测,节日期间这种鲜花的需求量X服从如下表所示的分布:
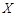 |
200 |
300 |
400 |
500 |
 |
0.20 |
0.35 |
0.30 |
0.15 |
若进这种鲜花500束,则利润的均值为()
A.706元 B.690元 C.754元 D.720元
在“信阳市中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )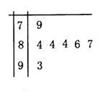
A.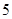 和 和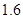 |
B. 和 和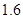 |
C. 和 和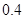 |
D.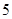 和 和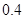 |