高中数学随机思想的发展解答题

有甲、乙两个建材厂，都想投标参加某重点建设项目，为了对重点建设项目负责，政府到两建材厂抽样检查，他们从中各取等量的样品检查它们的抗拉强度指数如下：

	110	120	125	130	135
P	0.1	0.2	0.4	0.1	0.2
	100	115	125	130	145
P	0.1	0.2	0.4	0.1	0.2

其中和分别表示甲、乙两厂材料的抗拉强度，在使用时要求抗拉强度不低于120的条件下，比较甲、乙两厂材料哪一种稳定性较好.

已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(2) $\xi$表示依方案乙所需化验次数,求 $\xi$的期望.

设随机变量具有分布P（=k）=，k=1，2，3，4，5，求E（+2）²，V（2-1），（-1）.

某运动员投篮时命中率p=0.6.
（1）求一次投篮命中次数的期望与方差；
（2）求重复5次投篮时，命中次数的期望与方差.

编号1,2,3的三位学生随意入座编号为1，2，3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的个数
是X.
（1）求随机变量X的概率分布；
（2）求随机变量X的数学期望和方差.

设离散型随机变量X的概率分布为

X	0	1	2	3	4
P	0.2	0.1	0.1	0.3	m

求：（1）2X+1的概率分布；
（2）|X-1|的概率分布.

某单位举办2010年上海世博会知识宣传活动，进行现场抽奖．盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”（世博会吉祥物）图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖，否则，均为不获奖．卡片用后放回盒子，下一位参加者继续重复进行．
（I）活动开始后，一位参加者问：盒中有几张“海宝”卡？主持人答：我只知道，从盒中抽取两张都是“世博会会徽”卡的概率是，求抽奖者获奖的概率；
（Ⅱ）现有甲乙丙丁四人依次抽奖，用表示获奖的人数，求的分布列及的值．

（本上题满分12分）某高校为了参加“CBA杯”安徽省大学生篮球联赛暨第十届CU—BA安徽省选拔赛，需要在各班选拔预备队员，规定投篮成绩甲级的可作为入围选手，选拔过程中每人投篮5次，若投中3次则确定为乙级，若投中4次及以上则可确定为甲级，一旦投中4次，即终止投篮，已知某班同学小明每次投篮投中的概率是0.6。（I）求小明投篮4次才被确定为乙级的概率； （II）设小明投篮投中次数为X，求X的分布列及期望。

一袋子中有大小相同的2个红球和3个黑球，从袋子里随机取球，取到每个球的可能性是相同的，设取到一个红球得2分，取到一个黑球得1分。（Ⅰ）若从袋子里一次随机取出3个球，求得4分的概率；（Ⅱ）若从袋子里每次摸出一个球，看清颜色后放回，连续摸3次，求得分的概率分布列及数学期望。

某中学在高一开设了数学史等4门不同的选修课，每个学生必须选修，有只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。（Ⅰ）求3个学生选择了3门不同的选修课的概率；（Ⅱ）求恰有2门选修课这3个学生都没有选择的概率；（Ⅲ）设随机变量为甲、乙、丙这三个学生选修数学史这门课的人数，求的分布列
与数学期望。

甲从装有编号为1，2，3，4，5的卡片的箱子中任意取一张，乙从装有编号为2，4的卡片的箱子中任意取一张，用，分别表示甲、乙取得的卡片上的数字.（1）求概率）；（2）记，求的分布列与数学期望.

一厂家向用户提供的一箱产品共10件，其中有2件次品，用户先对产品进行抽检以决定是否接收．抽检规则是这样的：一次取一件产品检查（取出的产品不放回箱子），若前三次没有抽查到次品，则用户接收这箱产品；若前三次中一抽查到次品就立即停止抽检，并且用户拒绝接收这箱产品.（1）求这箱产品被用户接收的概率；（2）记抽检的产品件数为，求的分布列和数学期望．

（本小题共13分）
　　一厂家向用户提供的一箱产品共10件，其中有2件次品，用户先对产品进行抽检以决定是否接收。抽检规定是这样的：一次取一件产品检查，若前三次没有抽查到次品，则用户接收这箱产品，而前三次中只要抽查到次品就停止抽检，并且用户拒绝接收这箱产品。
　　（I）求这箱产品被用户拒绝接收的概率；
　　（II）记表示抽检的产品件数，求的概率分布列。

(2009湖南卷理)（本小题满分12分）  
为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的.、、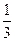，现在3名工人独立地从中任选一个项目参与建设。          
（I）求他们选择的项目所属类别互不相同的概率；
（II）记为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数，求 的分布列及数学期望。

2009全国卷Ⅱ理（本小题满分12分）
某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核。
（I）求从甲、乙两组各抽取的人数；     
（II）求从甲组抽取的工人中恰有1名女工人的概率；
（III）记表示抽取的3名工人中男工人数，求的分布列及数学期望。