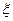
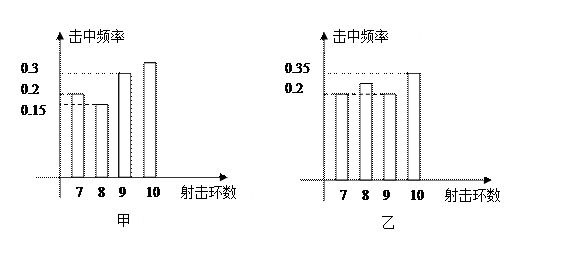
（1） 求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。
（2） 求甲运动员射击环数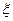的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？
，求cos2x和
值．
，
若
，
，求
的值。
，
．求
和
的值．
，
，
，
，求
的值.相关知识点
推荐套卷
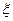
（1） 求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。
（2） 求甲运动员射击环数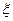的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？
粤公网安备 44130202000953号