如图 A B两点有5条线并联，它们在单位时间内能通过的信息依次为2、3、4、3、2，现从中任取三条线且记在单位时间内通过的信息总量为ζ。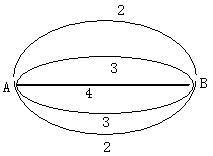
（Ⅰ）写出信息总量ζ的分布布列；
（Ⅱ）求信息总量ζ的数学期望。
相关试题
与
分别是实系数一元二次方程
和
的一个实根，且
，
．求证：方程
必有一根介于
的顶点分别为
，
在直线
上．
，求点
，求点
．
的最小正周期；
时，求
，求
的值．
，直线
过定点A(1，0)．
的交点为N，判断
是否为定值，若是，则求出定值；若不是，请说明理由．相关知识点
推荐套卷
如图 A B两点有5条线并联，它们在单位时间内能通过的信息依次为2、3、4、3、2，现从中任取三条线且记在单位时间内通过的信息总量为ζ。
（Ⅰ）写出信息总量ζ的分布布列；
（Ⅱ）求信息总量ζ的数学期望。
粤公网安备 44130202000953号