高中数学平行线法解答题

（本小题只理科做，满分14分）如图,已知平面,,△是正三角形,,且是的中点.

（1）求证:平面;
（2）求证:平面平面;
（3）求平面与平面所成锐二面角的大小.

（本小题满分14分）
在正三棱柱中，点是的中点，．
（1）求证：∥平面；
（2）试在棱上找一点，使．

（本小题满分12分）如图，已知PA⊥⊙O所在的平面， AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC=PA，E是PC的中点，F是PB的中点．

（1）求证：EF//平面ABC；
（2）求证：EF⊥平面PAC；
（3）求三棱锥B—PAC的体积．

己知四棱锥P-ABCD，其中底面ABCD为矩形侧棱PA底面ABCD，其中BC=2,AB=2PA=6，
M,N为侧棱PC上的两个三等分点，如图所示：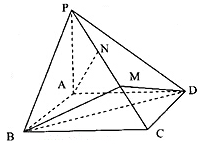

（1）求证：AN∥平面MBD；
（2）求二面角B-PC-A的余弦值．

如图，在直角梯形中，，，平面，，．

（Ⅰ）求证：平面；
（Ⅱ）在直线上是否存在点，使二面角的大小为？若存在，求出的长；若不存在，说明理由．

（本小题满分12分）
四棱锥S－ABCD中，侧面SAD是正三角形，底面ABCD是正方形，且平面SAD⊥平面ABCD，M、N分别是AB、SC的中点．
(Ⅰ)求证：MN∥平面SAD；
(Ⅱ)求二面角S－CM－D的余弦值．

（本小题满分12分）
如图，四边形ACDF为正方形，平面平面BCDE,平面平面ABC,BC=2DE,DE//BC， M为AB的中点.

（I）证明：；
（II）证明：EM//平面ACDF.

（本小题满分12分）
如图，ABCD为梯形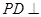，平面ABCD，AB//CD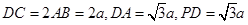，，E为BC中点

（I）求证：平面平面PDE；
（II）线段PC上是否存在一点F，使PA//平面BDF？若有，请找出具体位置，并进行证明；若无，请分析说明理由.

如图，四边形ABCD为梯形，AB∥CD， 平面ABCD，，
，E为BC中点。

（1）求证：平面平面PDE；
（2）线段PC上是否存在一点F，使PA//平面BDF？若存在，请找出具体位置，并进行证明；若不存在，请分析说明理由．

在四棱锥中，底面是正方形，侧棱底面， ，点是的中点，作交于.

（Ⅰ）求证：∥平面；
（Ⅱ）求证：平面；
（Ⅲ）求二面角的大小.

如图，在四棱锥中，平面平面为上一点，四边形为矩形，

（1）若 ， 且平面求的值；
（2）求证：平面

(本小题满分14分)如图，在三棱锥中，，点是线段的中点，平面平面．

（1）在线段上是否存在点， 使得平面？ 若存在， 指出点的位置， 并加以证明；若不存在， 请说明理由;
（2）求证：.

如图所示，直三棱柱中，是线段的中点，，。

(Ⅰ)证明：面；
(Ⅱ)求面与面所成的锐二面角的余弦值。      

（本小题满分14分）如图，菱形的边长为，，.将菱形沿对角线折起，得到三棱锥，点是棱的中点，.

（1）求证：平面；
（2）求三棱锥的体积.

（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）如图，四棱锥中，是正三角形，四边形是矩形，且平面平面，，．

（Ⅰ）若点是的中点，求证：平面；
（Ⅱ）若点在线段上，且，当三棱锥的体积为时，求实数的值.