山东省潍坊市高三上学期期末考试文科数学试卷B卷
下列说法中正确的是( )
A.命题“若 ”的逆否命题是“若 ”的逆否命题是“若 ,则 ,则 ” ” |
B.若命题 |
C.设l是一条直线, 是两个不同的平面,若 是两个不同的平面,若 |
D.设 ,则“ ,则“ ”是“ ”是“ ”的必要而不充分条件 ”的必要而不充分条件 |
定义在R上的偶函数 的部分图象如图所示产,则在
的部分图象如图所示产,则在 上,下列函数中与
上,下列函数中与 的单调性不同的是( )
的单调性不同的是( )
A. |
B. |
C. |
D. |
如图,向边长为2的正方形中随机投入一粒黄豆,若圆C的方程为 ,则黄豆落入阴影部分的概率为( )
,则黄豆落入阴影部分的概率为( )
A. |
B. |
C. |
D. |
某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料3千克,B原料1千克;生产乙产品1桶需耗A原料1千克,B原料3千克.每生产一桶甲产品的利润400元,每生产一桶乙产品的利润300元.公司在生产这两种产品的计划中,每天消耗A、B原料都不超过12千克,通过合理安排生产计划,公司每天可获得的最大利润是(单位:元)( )
A.1600 B.2100 C.2800 D.4800
已知 分别为双曲线
分别为双曲线 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________.
设函数 的定义域为D,若任取
的定义域为D,若任取 ,存在唯一的
,存在唯一的 满足
满足 ,则称C为函数
,则称C为函数 在D上的均值.给出下列五个函数:
在D上的均值.给出下列五个函数:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .则所有满足在其定义域上的均值为2的函数的序号为_________.
.则所有满足在其定义域上的均值为2的函数的序号为_________.
(本小题满分12分)
某中学举行了一次“社会主义核心价值观知识竞赛”活动,为了解本次竞赛中学生成绩情况,从全体学生中随机抽取了部分学生的分数(得分取整数且不低于50分,满分100分),作为样本(样本容量为n)进行统计.按照
 的分组作出频率分布直方图,并作出茎叶图(图中仅列出来
的分组作出频率分布直方图,并作出茎叶图(图中仅列出来 这两组的数据).
这两组的数据).
(I)求样本容量n和频率分布直方图中的 ;
;
(II)在选取的样本中,从样本中竞赛成绩80分以上(含80分)的同学中随机抽取2名同学到市政广场参加社会主义核心价值观知识宣传志愿者活动.求所抽取的2名同学来自不同组的概率.
(本小题满分12分)
已知函数
(I)求函数 上的最值;
上的最值;
(II)若将函数 的图象向右平移
的图象向右平移 个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到
个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到 的图象.已知
的图象.已知 的值.
的值.
(本小题满分12分)
各项均为正数的数列 的前
的前 项和为
项和为 ,已知点
,已知点 在函数
在函数 的图象上,且
的图象上,且
(I)求数列 的通项公式;
的通项公式;
(II)在 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
如图,四边形ACDF为正方形,平面 平面BCDE,平面
平面BCDE,平面 平面ABC,BC=2DE,DE//BC, M为AB的中点.
平面ABC,BC=2DE,DE//BC, M为AB的中点.
(I)证明: ;
;
(II)证明:EM//平面ACDF.
(本小题满分13分)
已知椭圆 的一个焦点和抛物线
的一个焦点和抛物线 的焦点相同,过椭圆右焦点F且垂直
的焦点相同,过椭圆右焦点F且垂直 轴的弦长为2.
轴的弦长为2.
(I)求椭圆C的方程;
(II)若与直线 相垂直的直线
相垂直的直线 与椭圆C交于B、D两点,求
与椭圆C交于B、D两点,求 的最大值.
的最大值.
 ( )
( )



 为纯虚数,则实数
为纯虚数,则实数 ( )
( )


 的直线与圆
的直线与圆 有公共点,则该直线的倾斜角的取值范围是( )
有公共点,则该直线的倾斜角的取值范围是( )








 ,则输出的
,则输出的 ( )
( )




 的各实根为
的各实根为 .若点
.若点 均在直线
均在直线 的同侧,则实数
的同侧,则实数 的取值范围是( )
的取值范围是( )



 ,
, __________.
__________. ___________.
___________. 中,角A,B。C的对边分别为
中,角A,B。C的对边分别为 .已知
.已知 ,则角A为__________.
,则角A为__________.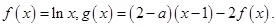
 时,求函数
时,求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数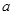 的最小值;
的最小值;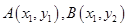 是函数
是函数 图象上任意不同两点,线段AB中点为C
图象上任意不同两点,线段AB中点为C ,直线AB的斜率为k.证明:
,直线AB的斜率为k.证明: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号