已知公比不为 的等比数列
的等比数列 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且 成等差数列.
成等差数列.
(1)求等比数列 的通项公式;
的通项公式;
(2)对 ,在
,在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数成等差数列,记插入的这
个数成等差数列,记插入的这 个数的和为
个数的和为 ,求数列
,求数列 的前
的前 项和
项和 .
.
设数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
设等差数列{ }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2,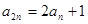 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设数列{ }满足
}满足 ,求{
,求{ }的前n项和Tn;
}的前n项和Tn;
(3)是否存在实数K,使得Tn 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由.
在等差数列{an}中, 为其前n项和
为其前n项和 ,且
,且
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
设数列{an}是等差数列,数列{bn}的前n项和Sn满足 且
且
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{Sn}的前n项和,求Tn.
右表是一个由正数组成的数表,数表中各行依次成等差数列,各列依次成等比数列,且公比都相等,已知

(1)求数列 的通项公式;
的通项公式;
(2)设 求数列
求数列 的前
的前 项和
项和 。
。
右表是一个由正数组成的数表,数表中各行依次成等差数列,各列依次成等比数列,且公比都相等,已知

(1)求数列 的通项公式;
的通项公式;
(2)设 求数列
求数列 的前
的前 项和
项和 。
。
已知等差数列 的前
的前 项和为
项和为 ,且
,且 .
.
(I)求数列 的通项公式;
的通项公式;
(II)设等比数列 ,若
,若 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知等差数列 满足:
满足: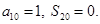
(1) 求数列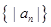 的前20项的和;
的前20项的和;
(2) 若数列 满足:
满足: ,求数列
,求数列 的前
的前 项和.
项和.
已知等差数列{an}的通项公式为 ,从数列{an}中依次取出a1,a2,a4,a8,…,
,从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.
已知数列{ }的前n项和
}的前n项和 ,数列{
,数列{ }满足
}满足 =
= .
.
(I)求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;
(Ⅱ)设 ,数列{
,数列{ }的前n项和为Tn,求满足
}的前n项和为Tn,求满足 的n的最大值.
的n的最大值.