高中数学数列综合解答题

已知等差数列的前四项和为10，且成等比数列
（1）求通项公式
（2）设，求数列的前项和

已知等差数列满足：，．的前n项和为．
（Ⅰ）求及；
（Ⅱ）令b_n=(nN^*)，求数列的前n项和．

已知是等差数列，其前项和为，已知
（1）求数列的通项公式；
（2）设，证明:是等比数列，并求其前项和.
(3) 设,求其前项和

）已知数列是等差数列，其前n项和为，，
（I）求数列的通项公式；
（II）设p、q是正整数，且p≠q. 证明：.

已知等差数列中，首项a₁=1，公差d为整数，且满足数列满足前项和为．
（1）求数列的通项公式a_n；
（2）若S₂为，的等比中项，求正整数m的值．

已知是首项为19，公差为-2的等差数列，为的前n项和。
（Ⅰ）求通项及；
（Ⅱ）设是首项为1，公比为3的等比数列，求数列的通项公式及其前n项和

已知等差数列{a_n}的前n项和为
(I)若a₁=1，S₁₀= 100，求{a_n}的通项公式;
(II)若=n²-6n，解关于n的不等式+ a_n >2n

等差数列{}的各项均为正数，＝3，前项和为，等比数列{}中，＝1，＝64，{}是公比为64的等比数列．
(Ⅰ)求与；
(Ⅱ)证明：＋＋＋…＋<.

已知数列是等差数列,，数列的前n项和是，且.
（I）求数列的通项公式；
（II）求证：数列是等比数列；

某市去年11份曾发生流感，据统计，11月1日该市新的流感病毒感染者有20人，此后，每天的新感染者平均比前一天的新感染者增加50人，由于该市医疗部门采取措施，使该种病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少30人，到11月30日止，该市在这30日内感染该病毒的患者总共8670人，问11月几日，该市感染此病毒的新患者人数最多？并求这一天的新患者人数.

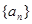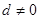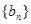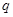设等差数列的公差，等比数列为公比为，且，，.
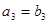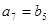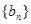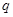（1）求等比数列的公比的值；
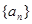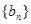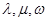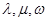（2）将数列，中的公共项按由小到大的顺序排列组成一个新的数列，是否存在正整数（其中）使得和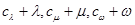都构成等差数列？若存在，求出一组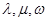的值；若不存在，请说明理由.

已知数列的前项和为，且满足 ()，，设，．
（1）求证：数列是等比数列；
（2）若≥，，求实数的最小值；
（3）当时，给出一个新数列，其中，设这个新数列的前项和为，若可以写成 (且)的形式，则称为“指数型和”．问中的项是否存在“指数型和”，若存在，求出所有“指数型和”；若不存在，请说明理由．

已知为等差数列，且
（1）求数列的第二项；
（2）若成等比数列，求数列的通项.

等差数列中，且成等比数列，
(1)求数列的通项公式；（2）求前20项的和。

已知各项均不相等的等差数列的前三项和为18，是一个与无关的常数，若恰为等比数列的前三项，（1）求的通项公式．（2）记数列，的前三项和为，求证：